L'essai de 1773 sur la statique – 3a Parte
Por: Santiago Osorio R.
Tercera parte de la quinta entrega de la serie 'DU PLAN INCLINÉ À LA
THÉORIE DU COIN DES TERRES' (Del plano inclinado a la teoría de la cuña de suelo), una visión detallada del aporte de Charles Augustin Coulomb a la consolidación de la teoría clásica de la mecánica de suelos.
Octubre 11 de 2021.
Las principales contribuciones de Coulomb en la primera parte de su carrera profesional fueron en el campo de la mecánica aplicada y la ingeniería, disciplina a la que ingresó en un momento en que sus mejores representantes se volcaban hacia lo que uno podría llamar una ingeniería racional en lugar de una ingeniería empírica tradicional. Sus estudios en el Collège Royal de France con Le Monnier y en la École du génie de Mézières con Bossut, lo ayudaron a obtener un mejor conocimiento de las matemáticas que el que poseían esos ingenieros practicantes de una generación anterior.
La experiencia adquirida en Martinica, en Cherbourg, y en muchos otros puestos en Francia le permitieron llevar a sus memorias de ingeniería un conocimiento realista del comportamiento de las estructuras y materiales y lo condujo a sus estudios fundamentales en resistencia de materiales, en la teoría de la presión de tierra y sobre la fricción.
En el momento de su elección a la Academia, Coulomb ya había ganado renombre como ingeniero. Cuando luego se concentró en la física, tanto su formación matemática como su experiencia en ingeniería apoyó sus investigaciones físicas de manera rentable y condujo directamente a sus descubrimientos en torsión e indirectamente a su cuantificación de los campos de la electricidad y el magnetismo.
El bicentenario del ensayo de Coulomb se celebró en 1973 en el VII Congreso Internacional de Mecánica de Suelos en Moscú. Su vida y obra se
describen en detalle en el libro de Gillmore (1971), pero es en el libro
del profesor Heyman (1972) donde es extraído el significado pleno de ese
ensayo, que va mucho más allá de la cuestión de los muros de contención. A
continuación, se reproducen los principales aspectos de los
prefacios de ambas publicaciones.
Algunos importantes apartes del prefacio de Charles Stewart Gillmor en su obra sobre C.A. Coulomb de 1971
“La ingeniería se desarrolló rápidamente a principios del siglo XVIII en
Francia, y para mediados del siglo había grupos bien establecidos de
hombres en varias disciplinas de ingeniería. Aun así, la formación
matemática de Coulomb en el College de France y en la Ecole du génie de
Mézieres le proporcionó los medios para abordar muchos problemas básicos
de ingeniería de nuevas maneras. Las matemáticas por sí solas no lo
convirtieron en ingeniero. Después de su graduación en de Mézieres, entró
en un período de veinte años de ingeniería en el campo, separado de París
y de la mayor parte de la actividad científica. Es durante este tiempo que
él ganó la experiencia que, junto con su uso del análisis racional, le
permitió concebir el estudio de los problemas de ingeniería a través de un
“mélange du calcul et de la physique.”
Ingresó en la Academia de Ciencias de Francia en 1781, pero fue elegido
por su reputación como ingeniero en lugar de físico. Su ingeniería, que se
había beneficiado de sus primeros trabajos en matemática, ahora contribuyó
a su desarrollo como físico. Biot dijo que se le debe a Borda y a Coulomb
el renacimiento de la física exacta en Francia. Delambre vio las
contribuciones de Coulomb a la física de la misma manera. Ambos hombres
aludían como “física” no a la mecánica racional, sino a los campos
emergentes de calor, luz, cristalografía, electricidad y magnetismo. La
física de Coulomb fue coloreada por su concepción del experimento. Llevó a
la experimentación física no solo su habilidad instrumental sino también
como conjunto de significado y realidad que obtuvo de su trabajo en
ingeniería.
Los veinticinco años de Coulomb como miembro de la Academia de Ciencias y
de su sucesor, el Instituto, tuvieron otros deberes además de los de
académico y físico. Participó en la administración de las aguas y fuentes,
la reforma de hospitales y el sistema de pesos y medidas, y después de la
Revolución, en la reorganización de la educación francesa.
Los estudios de Coulomb en física fueron fuertemente influenciados por su
trabajo inicial en mecánica aplicada e ingeniería. Él y algunos de sus
contemporáneos criticaron la naturaleza de algunas soluciones mecánicas
racionales respecto de los problemas físicos reales. También criticaron,
los experimentos a veces curiosos o inútiles de los primeros filósofos
naturales, practicantes de la physique générale, o personalidades del
cabinet de physique y el salon. Los mejores filósofos naturales de
comienzos del siglo XVIII, como Pieter van Musschenbroek (1692-1761) y
John Theophilus Desaguliers (1683-1744), rechazaron las hipótesis
especulativas y pidieron la física basada en el experimento. Al mismo
tiempo, Bernard Forest de Bélidor (1698-1761), Frézier, y otros escritores
de ingeniería llevaron a los ingenieros a la tarea de despedir la théorie
y tratar únicamente con la pratique. Sin embargo, cada uno de estos grupos
tendía a sobrestimar la facilidad con la que podían superarse los
problemas de su dualidad pratique-théorique. Ambos escribieron sobre la
mayoría o todas las cosas de interés; sus investigaciones eran a menudo
amplias, y sus redes demasiado gruesas.
El equilibrio de la física a menudo gira sobre pivotes de bordes finos.
Coulomb comprendió la importancia de explotar completamente la física de
la torsión en cilindros delgados y luego se movió para establecer
cuantitativamente la idea de las fuerzas centrales newtonianas en
electrostática y magnetismo en lugar de los vórtices y efluvios de
inspiración cartesiana, lo que marcó un importante paso en su evolución.
Coulomb pidió no solo la sofisticación de las técnicas matemáticas, sino
también la realidad en el experimento y en las hipótesis físicas. Como
indico más adelante, tal vez la filosofía natural dio la curiosidad, y la
ingeniería dio la realidad y la armonía del análisis racional que
caracteriza a la física.
… el período de aproximadamente 1775 a 1825 fue un momento emocionante
para la física. Lavoisier, Laplace, Monge, Borda: amigos cercanos, o
aquellos con quienes Coulomb trabajó, reconocieron esto. Lagrange también
lo reconoció cuando escribió con desánimo a d'Alembert en 1781: “La física
y la química ahora ofrecen riquezas más brillantes y más fáciles de
explotar; además, el sabor del siglo parece estar totalmente dirigido en
esta dirección, y no es imposible que las cátedras de Matemáticas
[Géométrie] en las Academias algún día ocuparán la misma posición
insignificante que las cátedras universitarias de árabe ocupan
actualmente.” [Oeuvres de Lagrange, XIII, 368.] La carrera de Charles
Augustin Coulomb se movió en el corazón de este período. Espero que el
lector comparta mi placer de seguirlo como ingeniero y físico en la
Francia del siglo XVIII.”
Algunos importantes apartes del prefacio de Jacques Heyman en su obra sobre C.A. Coulomb de 1972
“El Essai de Coulomb sobre “algunos problemas de la estática” es más
conocido como la memoria que sentó las bases de la ciencia moderna de la
mecánica del suelo; la revista Géotechnique, por ejemplo, usa el
cul-de-lampe (Figura 1) en la p. 40 del Essai en la portada de cada uno de
sus ediciones. Sin embargo, Coulomb discute en el mismo documento otros
tres problemas principales de la ingeniería civil del siglo XVIII, a
saber, la flexión de vigas, la fractura de columnas y el cálculo de los
empujes de pilares desarrollados por los arcos de mampostería.
… el capítulo (5) señala la primera aplicación de los principios de la
mecánica a la evaluación de las presiones de tierra (por Bullet en 1691),
y luego sigue el hilo de este trabajo a través del siglo XVIII hasta
Coulomb. La historia continúa en el siglo XIX hasta que la teoría ha
alcanzado una forma (con Boussinesq en 1882) que es reconociblemente
moderna. Hay una breve discusión sobre el trabajo de Sokolovskii en el
presente siglo, que representa el desarrollo final de este tipo de teoría.
En todo el capítulo 5 se supone que el suelo es un material de una fase,
con cohesión constante c y ángulo de fricción interna 𝜙; de hecho, esta
era la suposición de Coulomb. En la medida de lo posible, el tratamiento
se sitúa en el marco de los teoremas límite de la teoría de la
plasticidad, y en realidad es más cierto decir que, en lugar de seguir el
hilo desde 1691, los antecedentes de la teoría moderna de una fase se
remontan a Coulomb y más allá.
Desde que Terzaghi introdujo la idea del suelo como un material de dos
fases, se ha hecho evidente que el tratamiento monofásico es un modelo
pobre de muchos problemas en la mecánica del suelo; … Aunque los
ingenieros eran conscientes de la importancia del agua, hay muy poco en la
literatura más allá de las advertencias ocasionales (por ejemplo, por
Bossut en 1762, o por el propio Coulomb ...
Aunque algunos de los trabajos más antiguos parecen haber sido
recientemente redescubiertos aquí, todo este libro se apoya mucho en los
hallazgos de comentaristas anteriores. Poleni, Girard y Mayniel dan
interesantes relatos históricos iniciales sobre los problemas de los
arcos, la flexión de las vigas y la mecánica del suelo, respectivamente;
En el siglo XIX, tanto Augoyat como Maindron son útiles para comprender la
educación técnica francesa, un tema que ha sido tratado recientemente por
Artz. Las historias técnicas más recientes se citan en el texto y se
enumeran en las referencias; de estos, el relato de Truesdell de cuerpos
flexibles es definitivo.
Es interesante dar una explicación de la vida de Coulomb, y es muy
afortunado que el libro de Gillmor ya esté disponible. Los relatos
anteriores fueron superficiales, y las notas históricas incluidas en el
capítulo 7, aunque muy breves, se basan al menos en la investigación
directa de archivos.
Essai sur une application des regles de Maximis & minimis à quelques
problemes de statique, relatifs à l’architecture, Mémoires de Mathématique
y de Physique, présentés à l’Académie Royale des Sciences par divers
Savans, & lûs* dans ses Assemblées, vol. 7, 1773, pp. 343-82, Paris
(1776). Reimpreso en Théorie des machines simples, Paris (1821).
* La memoria de Coulomb fue leída por él el 10 de marzo y el 2 de abril de
1773.”
El profesor inglés Jacques Heyman (1925- ) sometió al profesor de la
Universidad de Cambridge Andrew Noel Schofield (1930- ) la revisión de los
borradores de su libro.
 |
Figura 1.
Cul-de-lampe de la Memoria sobre Estática
de Coulomb de 1773, publicada en 1776 |
La Ciencia hasta el siglo XVIII
Desde los filósofos griegos y hasta el siglo XVI los científicos se
preocuparon por integrar la observación con el razonamiento y la
verificación experimental. Fueron creadas universidades para estudiar
astronomía, medicina, matemáticas, y religión. Cuando el pensamiento
científico pasó de la teoría geocéntrica a la heliocéntrica (Figura 2) se
dio una explosión de experimentos, inventos, publicaciones, y expediciones
a lo largo del planeta para reafirmar o refutar los conocimientos. La
técnica ensayo-error alcanzaba un mayor nivel de refinamiento.
 |
Figura 2. Teorías geocéntrica (izquierda) y heliocéntrica
(derecha) |
A mediados del siglo XVI el papa Pablo IV (papado 1555-1559), apoyado por
el rey español Felipe II, emprendió una persecución activa de sospechosos
(iniciada en 1542 como la Inquisición romana por el papa Pablo III),
incluidos obispos, cardenales, científicos y pensadores (Inquisición
Romana 1542-1965). Encargó a la Congregación del Santo Oficio que
elaborara una lista de libros que atentaban contra la fe o la moral, y
aprobó y publicó el primer Índice de Libros Prohibidos en 1559. En
adelante, comenzó a considerarse como instrumento para regular el orden en
la Iglesia, la ortodoxia doctrinal y castigar el Protestantismo; por
ejemplo, procesó y condenó a Galileo en 1633. El argumento fundamental de
la Iglesia para rechazar las teorías científicas es que estaban en abierta
contradicción con las enseñanzas de la Biblia, que contienen la verdad
infalible de Dios.
La ciencia como construcción conceptual de la Naturaleza no parte de unas
premisas establecidas sino del razonamiento inductivo, basado en la
observación empírica. Sólo el análisis de las realidades concretas permite
formular hipótesis explicativas, que luego son de nuevo contrastadas con
los hechos para comprobar su verdad o su falsedad (Figura 3).
 |
Figura 3. Métodos de razonamiento científico |
El siglo XVII trae las primeras contribuciones literarias sobre ingeniería
de suelos y el siglo XVIII marca el comienzo de la Ingeniería Civil,
cuando la ciencia se toma como fundamento del diseño estructural. El siglo
XVIII es también llamado Siglo de las Luces, debido a que durante el mismo
surgió el movimiento intelectual conocido como Ilustración. Muchos de los
acontecimientos políticos, sociales, económicos, culturales e
intelectuales de este siglo han extendido su influencia hasta la
actualidad. Entre los principales hitos están: la máquina de vapor (1705),
L'Encyclopédie (1751), y la Revolución Francesa (1789). Tras el caos
político y militar vivido en el siglo XVII, el siglo XVIII, no carente de
conflictos, verá un notable desarrollo en las artes y las ciencias
europeas de la mano de la Ilustración, un movimiento cultural
caracterizado por la reafirmación del poder de la razón humana frente a la
fe y la superstición. Las antiguas estructuras sociales, basadas en el
feudalismo y el vasallaje, serán cuestionadas y acabarán por colapsar, al
tiempo que, sobre todo en Inglaterra, se inicia la Revolución industrial y
el despegue económico de Europa. Durante dicho siglo, la civilización
europea occidental afianzará su predominio en el mundo, y extenderá su
influencia por todo el orbe.
Antes del siglo XVIII el arte de la ingeniería geotécnica se basaba
únicamente en experiencias pasadas a través de una sucesión de
experimentación sin ningún carácter científico real, en civilizaciones
como las del Nilo (Egipto), el Tigris y el Éufrates (Mesopotamia), el
Huang Ho (Río Amarillo, China) y el Indo (India), que sabían de la
construcción de diques y exclusas a partir de los suelos encontrados en
las planicies de inundación fluviales. Los antiguos templos y monumentos
construidos en todo el mundo, involucraron el suelo y la roca de alguna
forma. Los aztecas construyeron templos y ciudades sobre suelos muy pobres
en el Valle de México mucho antes de la llegada de los españoles al así
llamado Nuevo Mundo.
Los arquitectos y constructores europeos durante la Edad Media,
aprendieron acerca de los problemas de los asentamientos de las catedrales
y de los grandes edificios. El ejemplo más notable es la Torre Inclinada
de Pisa, cuya construcción comenzó en 1173 d.C., y se asentó debido a un
problema relacionado con la capacidad de carga del suelo. Los vikingos de
Escandinavia utilizaron pilotes de madera para apoyar las casas y las
estructuras de muelles sobre sus arcillas blandas. El “diseño” de las
fundaciones y otras construcciones que implicaban el suelo y la roca era
por reglas empíricas, y la primera teoría, como tal, se desarrolló hasta
mediados del siglo XVIII.
Coulomb es el nombre de ingeniería más famoso de la época. Él investigó
los problemas de presión de tierras en contra de los muros de contención,
y algunos de sus procedimientos de cálculo están todavía en uso todavía.
La teoría más común para la resistencia al corte de los suelos lleva su
nombre. Al observar la resistencia de los muros de contención y al someter
modelos a escala a experimentos basados en análisis retrospectivo, se
inició el desarrollo de una teoría de la presión del suelo. Las
publicaciones de Gauthier (1717), Belidor (1729), Sallonyer (1767),
Coulomb (1773), Papacino (1781), Prony (1802), Mayniel (1808), Français
(1820), Navier (1833), Poncelet (1840), Hope (1845), Rankine (1862),
Darwin (1883), Boussinesq (1876, 1882 y 1883) son los principales hitos de
la larga historia de investigación sobre muros de contención.
El Período Preclásico de la Mecánica de Suelos – Hasta el siglo XVIII
El período Preclásico cubre la mayor parte del siglo XVIII, solo
continuaba el siglo anterior de muchas maneras. Durante este período se
desarrollaron teorías empíricas de empuje de tierras basadas en la
observación. Precisar un comienzo siempre es complicado. Este es el caso
de la primera fase de la mecánica de suelos clásica. Aquel cuyo nombre
retiene la posteridad, sin querer menoscabar sus méritos, es parte de la
continuidad de la acumulación de conocimientos a la que dará un salto
desde un análisis y una síntesis que él mismo sólo debe a su talento,
incluso a su ingenio. Pero el período en el que intervino, la urgencia de
los avances a realizar, las condiciones económicas y sociales de su
tiempo, y el material acumulado por sus predecesores tampoco fue
indiferente a su éxito.
Esta parte de la historia temprana del conocimiento y comprensión de las
propiedades físicas y mecánicas del suelo, en términos de ingeniería, se
caracterizó por teorías semi-empíricas de presión de tierra basadas en
estudios de la ‘pendiente natural’ (Figura 4) y el peso unitario de los
materiales para relleno de tierra y varios tipos de suelos. También pueden
encontrarse ejemplos de diseños racionales en la construcción de cimientos
y presas de tierra, basados en sólidos juicios de ingeniería.
 |
Figura 4. Ángulo de reposo o pendiente natural de
algunos materiales y casos de aplicación en la geotecnia |
En 1717, el ingeniero real francés, Henri Gautier (1660-1737), estudió las
pendientes naturales de los suelos cuando se apilaron en un montón para
formular los procedimientos de diseño de muros de contención. La pendiente
natural es lo que ahora llamamos ángulo de reposo. Según este estudio, la
pendiente natural de arena limpia seca y tierra ordinaria fue de 31° y
45°, respectivamente. Además, se recomendó que el peso unitario de la
arena seca limpia y la tierra ordinaria fuera de 18,1 kN/m3 (1,846 ton/m3
o 115 lb/ft3) y 13,4 kN/m3 (1,366 ton/m3 o 85 lb/ft3), respectivamente. No
se informaron resultados de pruebas en arcilla. En 1729, Bernard Forest de
Bélidor (1698-1761) publicó en Francia La science des ingénieurs, un libro
de texto para ingenieros militares, en el cual propuso una teoría de la
presión lateral de tierra en los muros de contención que dio continuidad
al estudio original de Gautier (1717). También especificó un sistema de
clasificación de suelos. Los primeros resultados de la prueba de un modelo
de laboratorio en un muro de contención de 76 mm de alto (3 pulgadas)
construido con relleno de arena fueron reportados en 1746 por el ingeniero
francés, François Gadroy (1705-1759), quien observó la existencia de
planos de deslizamiento en el suelo al fallar. El estudio de Gadroy fue
resumido más tarde por J. J. Mayniel en 1808.
Esta acumulación de conocimientos previos es el caso de la tesis de
Coulomb (1736-1806) que no surgió de la nada, sino que se nutrió de un
conjunto de observaciones, pruebas e hipótesis, para las cuales fueron de
gran importancia los aportes de Vauban (1633-1707), Gauthier (1660-1737),
Bélidor (1698-1761), Gadroy (1705-1759), Perronet (1708- 1794) y el abad
Bossut (1730-1814), quien realizó pruebas de fricción y cohesión y fue
profesor de Coulomb en la Escuela de Ingeniería de Mézières. Las nociones
de cuña de tierra o prisma de empuje, de pendiente natural fueron fruto de
análisis y reflexiones previas. Tampoco es indiferente que, desde las
primeras páginas de su tesis, Coulomb se refiera a pruebas de fricción,
realizadas por Amontons (1663-1705), informes sobre pruebas de medición de
la cohesión a partir de la ruptura de diferentes probetas de material
hechas por él mismo, o en un pilar cuadrado estudiado por Musschenbroëk
(1692-1761). Su análisis se basó en un enfoque experimental que era la
regla en ese momento. La importancia de la tesis de Coulomb, que fue más
allá de la mecánica del suelo, pero que aportó elementos esenciales para
la reflexión tanto en el diseño de las bóvedas como en el de las vigas,
fue tal que se necesitaron varias décadas para fuera asimilada.
Durante este período, la mayoría de los desarrollos en el área de la
ingeniería geotécnica provino de ingenieros y científicos en Francia. En
el período preclásico, prácticamente todas las consideraciones teóricas
utilizadas para calcular la presión lateral de tierra en los muros de
contención se basaban en una superficie de falla en el suelo basada
arbitrariamente. En su Memoria sobre Estática presentada en 1773, el
ingeniero francés Charles Augustin Coulomb (1736–1806) utilizó los
principios del cálculo de máximos y mínimos para determinar la verdadera
posición de la superficie deslizante en el suelo detrás de un muro de
contención. En este análisis de equilibrio límite en mecánica de suelos,
Coulomb utilizó las leyes de fricción y cohesión para cuerpos sólidos.
Sobre el estudio de la presión de tierra contra los muros de contención verticales en la Mémoire de Coulomb de 1773
La resistencia de las vigas y la resistencia de las columnas son dos de
los cuatro problemas “clásicos” de la ingeniería civil del siglo XVIII.
Los otros dos temas son el empuje del suelo y el empuje de los arcos, y
los cuatro son abordados por Coulomb en su primera Mémoire publicada, la
de 1773.
Coulomb posiblemente había pasado por la escuela de La Fere, unos 40 años
después de que Bélidor comenzara a enseñar allí; ciertamente se unió a la
escuela de posgrado, la Ecole du Corps Royale du Génie, en Mézières, en
1760. Es probable que Bélidor fuera el libro de texto de la escuela;
Coulomb conocía el trabajo anterior de Vauban (1704, 1706), que había
tabulado los espesores de los muros de contención, y las pruebas
realizadas por Musschenbroek. Sin embargo, su conocimiento de la ciencia
de la ingeniería civil probablemente no era mucho más amplio de lo que
implican estas referencias.
Coulomb fue enviado a Brest después de graduarse de la Escuela de
Ingenieros Militares de Mézières en Francia a la edad de 26 años. Dos años
más tarde, en febrero de 1764, un barco navegaba hacia la isla caribeña de
Martinica y el oficial de ingeniería que había sido asignado al servicio
en el extranjero cayó enfermo. Coulomb fue reclutado en su lugar con muy
poca antelación, y no fue hasta junio de 1772 que logró regresar a
Francia. Sus deberes en Martinica incluían el diseño y la construcción de
fortificaciones para defender la isla contra un posible nuevo ataque de
los ingleses, y tal vez no sea sorprendente que, como joven egresado de la
universidad, descubrió que lo que le habían enseñado era insuficiente para
sus tareas. En el proceso de finalizar el diseño del fuerte, se sintió
insatisfecho con las reglas generales para dimensionar los muros de
contención porque dictaban que los muros eran demasiado grandes e iban en
contra de la política de austeridad estatal. Aunque ya se habían intentado
algunos análisis teóricos, eran defectuosos. Más tarde escribió:
“A menudo me he encontrado con situaciones en las que todas las teorías
basadas en hipótesis o en experimentos a pequeña escala en un laboratorio
de física han resultado inadecuadas en la práctica.”
Fue durante los ocho años en Martinica que Coulomb intentó encontrar
soluciones a los cuatro problemas clásicos incluyendo las presiones
laterales de tierra; escribió la Memoria, fechada y presentada en 1773,
para su propio uso (como él mismo dice en la introducción del ‘Essai’), en
espera que la Académie encuentre útil su pequeña contribución al monumento
del aprendizaje; el gran diseño está en manos de grandes hombres, pero los
trabajadores menores, escondidos en la oscuridad de los cimientos, quizás
también puedan ser de ayuda. Este trabajo es generalmente reconocido como
la primera contribución cuantitativa importante a lo que se convertiría en
ingeniería geotécnica. Coulomb fue el primero en definir la resistencia
del suelo utilizando tanto la cohesión como la fricción, el primero en
considerar la fricción del muro y el primero en buscar analíticamente la
orientación del plano de falla más crítico.
Coulomb leyó su artículo en la Academia el 10 de marzo y el 2 de abril de
1773. Fue revisado, un año después, por Bossut y Borda y publicado en
1776. Siendo una contribución de fundamental importancia en la ciencia de
la ingeniería civil, el artículo trata sobre la resistencia al corte de
mampostería y suelos, presión de tierra, estabilidad de arcos y
resistencia de vigas.
La sección más famosa de la Mémoire es la que trata sobre el empuje del
suelo, y Coulomb es considerado el fundador de la ciencia de la mecánica
de suelos; de hecho, la mecánica racional se había aplicado al problema
desde al menos 1691 (Bullet). Sin embargo, la contribución fundamental de
Coulomb fue asumir que la falla se produjo por cortante a lo largo de un
plano y determinar la posición de ese plano mediante el uso de “principios
de máximo y mínimo”.
En la convocatoria de trabajos del VII Congreso Internacional de
Mecánica de Suelos en Moscú en 1973, se reprodujo una de las figuras
principales del ensayo de Coulomb (Figura 5). 'La fuerza A' (muro),
escribe Coulomb "debe ser capaz de soportar ... todas las superficies CBeg
delimitadas por cualquier curva Beg, que, sostenida por su cohesión y su
fricción y sobre la que actúa su propio peso, ejercería el mayor empuje".
De esta afirmación quedará claro que, si se aplicara una fuerza en F
infinitesimalmente menor que la requerida para soportar la superficie de
mayor empuje, la masa de suelo podría dividirse solo a lo largo de esa
curva, mientras que todas las demás partes permanecerían unidas por
cohesión y por fricción. Así, para encontrar la fuerza A suficiente para
soportar toda la masa, se debe buscar esa superficie, entre todas las
fuentes CBeg, para las que el empuje en la línea CB es máximo. De manera
similar, para encontrar la mayor fuerza que puede actuar a través de F sin
perturbar el equilibrio, otra curva Be’g’ es un mínimo. Los límites de la
fuerza horizontal que se puede aplicar en F sin mover el suelo estarán
delimitados por los límites A y A', donde A será un máximo y A' un
mínimo'. Aquí Coulomb opone los casos activo y pasivo y muestra que los
límites para este último (mucho mayores) se derivan de un estudio del
mínimo, y viceversa.
 |
Figura 5. Esquema básico de análisis del empuje de
tierra de Coulomb |
Coulomb asume que la curva que da la fuerza A es una línea recta, la
experiencia demuestra que la superficie que se rompe es muy cercana a la
triangular. No hace la misma suposición para el caso pasivo: las curvas
Beg y Be'g' que dibuja a modo de ejemplo se curvan ligeramente. De hecho,
la curva para los valores habituales de 𝜙 es incluso más redondeada que
las dibujadas.
Coulomb llama la atención sobre el hecho de que se ha descuidado la
fricción creada sobre el muro de contención, y luego escribe:
"En el momento de la ruptura, el suelo está a punto de deslizarse a lo
largo de CB, lo que disminuye A y al mismo tiempo aumenta el momento del
muro de contención".
Este problema de fricción en el muro ocupó a los investigadores durante
los siguientes doscientos años. Rankine (1857) aplicó su teoría del campo
de esfuerzos para suelos sin cohesión que conduce a la expresión familiar
para un muro vertical y un suelo horizontal, lo que confirma el valor de
Coulomb para el estado activo.
La idea, en el fondo racional, de que el empuje de tierra no tiene la
dirección del plano de la pendiente (talus), sino una dirección que
depende de la fricción suelo-muro llevó a Coulomb a la solución del
problema. El Método de Coulomb consiste en determinar, entre todas las
cuñas CBa (Figura 5) que se obtienen cuando el ángulo de la cuña α en (a)
varía, el que produce el empuje más fuerte sobre el muro ECDG, teniendo en
cuenta tanto la fricción en el plano de deslizamiento como la fricción
entre suelo-muro.
En palabras de Coulomb:
"Si de hecho suponemos un triángulo rectángulo sólido, uno de cuyos lados
es vertical, y cuya hipotenusa toca un plano inclinado, sobre el cual el
triángulo tiende a deslizarse; si este triángulo, solicitado por su
gravedad, está sostenido por una fuerza horizontal, por su cohesión y por
su fricción, que actúan a lo largo de esta hipotenusa, fácilmente
determinaremos, en el caso de equilibrio, esta fuerza horizontal, por los
principios de la Estática. Si luego notamos que los terrenos, asumiéndolos
homogéneos, pueden separarse en caso de ruptura, no solo a lo largo de una
línea recta, sino a lo largo de cualquier línea curva; se sigue que para
tener la presión de una superficie de tierra contra un plano vertical, es
necesario encontrar entre todas las superficies descritas en un plano
vertical indefinido, la que, solicitada por su gravedad, y retenida por su
fricción y su cohesión, requeriría, para su equilibrio, estar sostenido
por una fuerza horizontal, que era un “máximo”; porque, pues entonces es
obvio que cualquier otra figura que requiera una fuerza horizontal menor,
en el caso de equilibrio, la masa adherente no podría dividirse. Como el
experimento produce aproximadamente una línea recta para la línea de
ruptura del suelo, cuando pierde su contención, en la práctica basta
buscar en una superficie indefinida, entre todos los triángulos que
presionan un plano vertical, que requiere, para ser sostenido, la mayor
fuerza horizontal. Tan pronto como se determina esta fuerza, las
dimensiones de los muros de revestimiento (contención) se pueden deducir
fácilmente."
La cuña de tierra es solicitada por dos fuerzas: su propio peso y la
reacción del muro (igual y opuesta al empuje de tierra); si no se tiene en
cuenta la fricción que se ejerce entre el paramento del muro y el suelo,
esta reacción se dirige horizontalmente. Estas fuerzas pueden
descomponerse en un componente perpendicular al plano de la pendiente y
otro paralelo al mismo. La ecuación que permite determinar el valor del
empuje se obtiene mediante un “criterio de resistencia”: la suma de los
componentes de las acciones según el plano de deslizamiento, teniendo en
cuenta también las fuerzas de fricción, debe ser igual a la resistencia
límite del suelo a la ruptura.
Coulomb define dos valores límite entre los que necesariamente debe variar
la cantidad de empuje del suelo. Si la reacción opuesta por el muro es
menor que el límite inferior, entonces en un cierto plano dentro del
triángulo CBa (Figura 5) la acción del suelo excede tanto la fuerza de
fricción como la cohesión, se produce la ruptura y el muro cede. Si, por
el contrario, esta reacción es mayor que la resistencia del suelo (límite
superior), ocurre el fenómeno contrario y el suelo refluye bajo la acción
del muro.
En el caso en que prevalezca la acción del suelo, el plano del talud
coincide con la superficie de deslizamiento, y es legítimo asumir que este
plano pasa por el ángulo interno (E) del pie del muro. Por el contrario,
no es posible saber exactamente qué sucede en la situación opuesta. Es por
ello que Coulomb no admite a priori la forma de la superficie de
deslizamiento, e invita a investigar la forma de esta superficie indicando
que se trata de uno de los problemas fundamentales si queremos comprender
completamente el complejo comportamiento mecánico del suelo. Sin embargo,
para llegar simplemente a fórmulas útiles para calcular muros de
contención, Coulomb considera que la superficie de deslizamiento es plana.
"Suponiendo que un triángulo rectangulo CBa, sólido y pesado, está apoyado
sobre la línea Ba por una fuerza A aplicada en F, perpendicular a la
vertical CB; que al mismo tiempo es solicitado por su peso φ, y retenido
sobre la línea Ba, por su cohesión con esa línea, y por la fricción. O
bien hecho CB ... a, Ca..x ;; δ(aa + xx)1/2 expresará la adherencia de la
línea aB; φ, peso del triángulo CBa, será igual a gax/2, donde g expresa
la densidad del triángulo.
Si descomponemos la fuerza A y la fuerza φ en dos direcciones, una
paralela a la línea Ba, la otra perpendicular a ella, los triángulos
φGδ.Fπp, que expresan estas fuerzas descompuestas, serán similares al
triángulo CaB, tendremos por tanto para estas fuerzas las siguientes
expresiones,
Pero si suponemos que la fuerza aplicada en F, llega a aumentar, al punto
que está lista para poner el mismo triángulo en movimiento en la dirección
Ba; por lo tanto, al nombrar A' esta fuerza, tendremos (...)
una cantidad que sería infinita si x es igual a a/n".
Entonces A y A' representan los límites superior e inferior del empuje.
Obviamente tenemos equilibrio si el valor del empuje está contenido dentro
del intervalo (A; A') para cualquier valor de x⸦ℜ, porque cualquiera que
sea el plano de deslizamiento, la acción no excede la resistencia debido a
la fricción y la cohesión. Pero si hay un valor de x para el cual la
acción ya no se encuentra dentro de los límites impuestos, entonces el
equilibrio ya no es posible. Por tanto, podemos obtener el valor más bajo
del empuje representando un máximo y el valor más alto si elegimos x tal
que A’ sea un mínimo.
Para el límite inferior, el único considerado por Coulomb, tenemos
Con esta expresión, que es independiente del esfuerzo tangencial límite δ,
Coulomb obtiene el valor correspondiente de A:
donde m y l son coeficientes constantes dependientes de la cantidad 1/n
que representa con precisión el coeficiente de fricción estática. Esta
fuerza será suficiente para soportar una masa CBlg indefinida. El momento
generado por el empuje A es igual a
y será igual al momento estabilizador producido por el peso del muro. "En
cuanto a la forma y dimensiones de los revestimientos (muros de
contención), concluye Coulomb, no hay nada mejor para consultar en este
género que las Recherches sur la figure des digues, obra que ya he citado’
(Coulomb se refiere al tratado de C. BOSSUT, G. VIALLET. Recherches sur la
construction la plus avantageuse des digues, Paris, 1764).
Coulomb desarrolló varios casos especiales: como el caso de un peso
concentrado que apoyado sobre el suelo, donde la hipótesis de una
superficie plana de deslizamiento parece menos justificada, o incluso en
el caso de fricción en la superficie de contacto entre el suelo y el muro.
Al estudiar la presión de tierra contra los muros de contención
verticales, Coulomb buscó incluir otro problema de ingeniería dentro de
los límites del cálculo variacional o cálculo de variaciones en donde se
buscan máximos y mínimos (denominados extremos relativos) de funcionales
continuos definidos sobre algún espacio funcional; este método corresponde
a una generalización del cálculo elemental de máximos y mínimos de
funciones reales de una variable.
El cálculo de variaciones se desarrolló a partir del problema de la curva
braquistócrona o cicloide (o curva del descenso más rápido, que es la
curva entre dos puntos que es recorrida en menor tiempo por un cuerpo que
comienza en el punto inicial con velocidad cero, y que debe desplazarse a
lo largo de la curva hasta llegar al segundo punto, bajo acción de una
fuerza de gravedad constante y suponiendo que no existe fricción (Figura
6), planteado inicialmente por Johann Bernoulli en 1696. Inmediatamente
este problema captó la atención de su hermano Jakob Bernoulli y del
Marqués de L'Hôpital, aunque fue Leonhard Euler el primero que elaboró una
teoría del cálculo variacional. Las contribuciones de Euler se iniciaron
en 1733 con su Elementa Calculi Variationum ('Elementos del cálculo de
variaciones') que da nombre a esta disciplina.
 |
Figura 6. La curva braquistócrona |
Al comparar la presión de tierra con los problemas de ingeniería
estructural Coulomb señaló en su Mémoire de 1773, “el Método es
absolutamente el mismo”. Como se describió antes, tanto el método
matemático como la concepción física eran iguales; Coulomb vio en ambos
casos el deslizamiento de una forma aproximadamente triangular a lo largo
de un plano de ruptura (Figura 7). La teoría de Coulomb relacionada con la
ruptura de los pilares de mampostería se refería a los materiales de
construcción, que observó que no se deslizaban a lo largo de una
superficie plana. La similitud conceptual entre esta teoría y la teoría de
la falla de tierra detrás de los muros de contención es evidente en el
ensayo de Coulomb
 |
Figura 7. Método de análisis utilizado por Coulomb en su ‘Essai’.
(a) Esquema de Coulomb que ilustra su teoría de presión de tierra. (b) Esquema
de Coulomb para la ruptura de columnas de mampostería, rotada 90° |
Todos los demás investigadores, incluido Bélidor, habían asumido que el
banco de tierra se rompía y se deslizaba a lo largo de un plano inclinado
sobre el ángulo de reposo del suelo. Coulomb, sin embargo, señaló que la
ruptura ocurre en dos etapas. El ángulo de reposo de un banco de tierra
auto soportado no es el mismo que el ángulo de formación del plano de
ruptura. Cualquiera que sea el ángulo de reposo después de que el muro se
derrumba o se separa del banco de tierra, este ángulo puede obtenerse solo
después de que la cuña de tierra deslizante haya movido el muro de
contención. Por lo tanto, los supuestos de 45° o 60° para el plano de
ruptura eran completamente arbitrarios. Suponiendo tierra homogénea y
fuerzas retardantes debidas a la cohesión y la fricción, Coulomb buscó el
ángulo (CBa en las Figuras 5 y 7(a)) bajo el cual el suelo se agrietaría.
Coulomb escribió el 'Essai' con muy pocos resultados prácticos para
guiarlo. Aunque trabajó en términos generales con un ángulo de fricción
arbitrario, no es sorprendente que haya usado 45° en sus ejemplos. Del
mismo modo, está muy listo para establecer la cohesión igual a cero al
hacer cálculos prácticos. Sin embargo, es, por supuesto, precisamente la
introducción de dos parámetros c y 𝜙 que describen las propiedades del
suelo lo que es de suma importancia en el análisis de Coulomb.
Dado que el sistema se investiga en un estado de equilibrio, el diagrama
de fuerza de Coulomb está cerrado. Consta de tres fuerzas:
1. A, la reacción horizontal del muro (aplicada en F en la Figura 5);
2. φ, el peso de la cuña de tierra deslizante; y
3. R, la reacción debida a la fricción y la cohesión.
Ahora, si este fuera el caso hidrostático donde la fricción y la cohesión
se suponen cero, entonces solo podría haber un valor de equilibrio para la
fuerza A. Es decir, si la fuerza aumentara, el nivel del fluido ideal
aumentaría; si disminuyera, caería. Para el caso de sólidos o semisólidos,
la existencia de fuerzas de fricción y cohesión amplía la curva Ba (Figura
5) a una familia de curvas situadas entre los límites Ba y Bg'. Coulomb
observó que en este caso real uno puede aplicar una variedad de fuerzas
entre los límites A y A' sin hacer que la cuña de tierra se mueva. Las
fuerzas de fricción deben ser superadas tanto para el movimiento hacia
arriba como hacia abajo. Para resolver estos límites, Coulomb equiparó las
fuerzas y encontró las condiciones límite donde A es un mínimo y A' un
máximo. Aquí solo le preocupaba la fuerza mínima necesaria para evitar que
la cuña se deslizara hacia abajo, por lo que resolvería solo la fuerza A.
Coulomb utilizó el coeficiente de fricción (1/n) como igual a la tangente
de lo que hoy se llama el ángulo de fricción interna. Por lo tanto, en la
forma moderna de la “Ecuación de Coulomb” con respecto a la resistencia al
corte, tan 𝜙 se sustituye por 1/n. La “Ecuación de Coulomb” moderna es
donde:
τ = Resistencia al corte
c = Cohesión
σ = Esfuerzo normal efectivo de la superficie de deslizamiento
𝜙 = Ángulo de fricción interna.
Coulomb observó que la curva de ruptura no necesita ser una línea recta,
sino que podría ser cualquier curva, pero como en el caso de la ruptura de
los pilares de mampostería (Figura 7(b)), citó la experiencia para
demostrar que la ruptura siempre ocurre en una curva que se aproxima mucho
a una línea recta. Descubrió que la cohesión tenía poco efecto sobre la
curva de ruptura en comparación con el efecto de la fricción. En suelos
con poca fricción (como arena seca), la curva de ruptura asumirá un ángulo
de 45°.
Como se indicó antes, para determinar las dimensiones reales del muro de
contención, es necesario encontrar el momento producido por la fuerza A
(aplicado en F en la Figura 5) alrededor del punto E, la base del muro. Al
integrar, Coulomb encontró que el momento alrededor del punto E debe ser
igual o superior al momento de la fuerza A para que exista equilibrio.
donde:
b = peso total del muro CE,
δ = cohesión;
l, m = coeficientes de fricción constantes.
Coulomb luego procedió a calcular algunos ejemplos de su método. Obtuvo
una relación de altura de muro respecto a la base de 7:1. Señaló que
Vauban recomendaba una proporción de 5:1 para casi todos los fuertes que
construyó y que agregó contrafuertes a los muros para obtener resistencia
adicional.
Coulomb defendió cortésmente los conservadores diseños de Vauban con la
afirmación:
“Este aumento de la resistencia no debe ser considerado como superfluo en
fortificaciones, donde los muros exteriores no deben ser derrumbados por
el primer disparo de cañón.”
Tenía un sentido tanto de la teoría como de la práctica. Por ejemplo, en
su ‘Essai’ también habló de los efectos perjudiciales del agua subterránea
y señaló:
“Aunque, para evitar este problema, en la práctica se colocan tuberías
verticales detrás de muros de contención, y los desagües a los pies de los
mismos muros, para que el agua pueda escurrir, estos desagües se bloquean,
ya sea por el suelo arrastrado con el agua o por el hielo, y a veces se
vuelven inútiles.”
A pesar de que el trabajo de Coulomb proporcionó importantes conocimientos sobre
el problema de la presión de tierra, fue difícil de aplicar a problemas
prácticos porque nadie tenía la capacidad de medir la cohesión y el ángulo
de fricción de un suelo. Las primeras pruebas importantes de resistencia
del suelo no se realizarían hasta unos 70 años después por otro francés,
Alexandre Collin, y el trabajo de Coulomb no fue ampliamente reconocido.
En la práctica, el trabajo de Coulomb no alcanzó su máximo potencial hasta
el siglo XX, cuando las pruebas de resistencia del suelo se hicieron
comunes.
Referencias
Benvenuto, E. (1991). An Introduction to the History of Structural
Mechanics. Part I: Statics and Resistance of Solids. Springer.
Benvenuto, E. (1991). An Introduction to the History of Structural
Mechanics. Part II: Vaulted Structures and Elastic Systems. Springer.
Bordes, J.L. (2000). Regard sur le passé de la géotechnique. Revue
Française de Géotechnique. 2e trimestre 2000. Pag. 13-26.
Coduto, D. (2001). Foundation Design: Principles and Practices.
Coduto, D. P., Yeung, R. M., Kitch, W. A. (2011). Geotechnical
Engineering: Principles and Practices, 2nd Edition. Pearson Education,
Inc.
Coulomb, C. A. (1776). “Essai sur une Application des Règles de Maximis et
Minimis á quelques Problemes de Statique, relatifs à l’Architecture”. Mem.
Div. Sav. Académie des Sciences.
Cuizon, S. A. (2015). Introduction to Soil Mechanics. Technological
University of the Philippines.
Das, B.M. (2009). Principles of Geotechnical Engineering. 7th Edition.
Pgs. 4-7.
Duque, G., Escobar, C. E. (2002). Mecánica de Suelos. Universidad Nacional
de Colombia Sede Manizales. En:
https://godues.blogspot.com/2010/08/libro-mecanica-de-los-suelos-gonzalo.html
Gillmor, C. S. (1968). “Charles Augustin Coulomb: Physics and Engineering
in Eighteenth-Century France,” PhD dissertation, University of Princeton.
Gillmor, C. S. (1971). Coulomb and the Evolution of Physics and
Engineering in Eighteenth-Century France, Princeton University Press,
Princeton, New Jersey, U.S.A.
de Boer, R. (2000). Theory of Porous Media: Highlights in Historical
Development and Current State. Springer. Verlag. Berlin. Heidelberg. New
York.
Heyman, J. (1972). Coulomb's Memoirs on Statics: An Essay in the History
of Civil Engineering. Cambridge, U.K.
Heyman, J. (1998). Structural Analysis. A Historical Approach. Cambridge
University Press.
Holtz, Robert D., Kovacs, William D. & Sheahan, Thomas C. An
Introduction to Geotechnical Engineering. 2nd Edition. Prentice Hall.
2011.
Kerisel, J. (1993). Retaining Structures: Proceedings of the Conference
Retaining Structures. Editor C. R. I. Clayton, Institution of Civil
Engineers (Great Britain). Thomas Telford, London.
McKyes, E. (1989). Agricultural Engineering Soil Mechanics. Elsevier.
Punmia, B.C., Jain, A.K. (2006). Soil Mechanics and Foundations. 17th Ed.
Laxmi Publications Ltd.
Radelet-de Grave, P. & Benvenuto, E. eds. 1995. Entre Mecanique et
Architecture - Between Mechanics and Architecture. Basel; Boston; Berlin:
Birkhäuser
Skempton, A. W. (1979). Landmarks in early soil mechanics. Jalons dans les
premiers siécles de la mécanique des sols. Proc. 7th Eur. Conf. Soil
Mech., Brighton, 1979, 5, 1-26.
Skempton, A. W. (1985). A History of Soil Properties, 1717-1927. Golden
Jubilee Volume. Proceedings of the Eleventh International Conference on
Soil Mechanics and Foundation Engineering, San Francisco, 12-16 august
1985.
Timoshenko, S. (1953). A History of Strength of Materials. With a brief
account of the history of theory of elasticity and theory of structures,
New York: McGraw-Hill Book Company.
Cita
Osorio, S. (2021). L'essai de 1773 sur la statique - 3a parte. Relatos de la Geotecnia. Blogger.com. geotecnia-sor2.blogspot.com. https://geotecnia-sor2.blogspot.com/2021/10/lessai-de-1773-sur-la-statique-3a-parte.html
Relatos de la Geotecnia
+ Apuntes de Geotecnia con Énfasis en Laderas
Ir a:
1 - Martinique, Antilles - France Février 1764 (Martinica, Antillas - Francia , febrero de 1764)
2 - Angoulême, province d'Angoumois - France 14 juin 1736 (Angoulême, provincia de Angumois - Francia, 14 de junio de 1736)
3 - Mézières, département des Ardennes - France 11 février 1760 (Mézières, departamento de Ardennes - Francia, 11 de febrero de 1760)
4 - Paris - France 10 mars 1773 (París - Francia, 10 de marzo de 1773)
5 - L'essai de 1773 sur la statique - 1a Parte (La Memoria sobre Estática de 1773 - 1a Parte)
6 - L'essai de 1773 sur la statique - 2a Parte (La Memoria sobre Estática de 1773 - 2a Parte)
8 - L'essai de 1773 sur la statique - 4a Parte (La Memoria sobre Estática de 1773 - 4a Parte)
9 - L'essai de 1773 sur la statique - 5a Parte (La Memoria sobre Estática de 1773 - 5a Parte)
10 - L'essai de 1773 sur la statique - 6a Parte (La Memoria sobre Estática de 1773 - 6a Parte)
11 - L'essai de 1773 sur la statique - 7a Parte (La Memoria sobre Estática de 1773 - 7a Parte)
12 - L'essai de 1773 sur la statique - 8a parte (La Memoria sobre Estática de 1773 - 8a Parte)
13 - La vie de Coulomb après l’Essai de 1773 (La vida de Coulomb posterior al 'Essai' de 1773)Apéndice A - Fuerte Bourbon (1765-1772)
Apéndice C - La Estática de las Siete Máquinas Simples
Apéndice D - La Statique (La Estática)
Apéndice E - Mécanique Classique (Mecánica Clásica)
Apéndice F - De la résistance des matériaux (De la Resistencia de Materiales)
Diseño: PatoMOP
2021
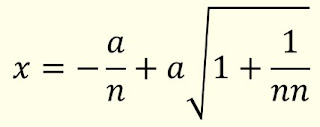
Comentarios
Publicar un comentario
Bienvenidos, agradezco sus comentarios ...