L'essai de 1773 sur la statique – 4a Parte
Por: Santiago Osorio R.
Cuarta parte de la quinta entrega de la serie 'DU PLAN INCLINÉ À LA THÉORIE
DU COIN DES TERRES' (Del plano inclinado a la teoría de la cuña de suelo), una visión detallada del aporte de Charles Augustin Coulomb a la
consolidación de la teoría clásica de la mecánica de suelos. Octubre 11 de
2021.
El estudio de la fricción de cuerpos sólidos tiene una historia de unos de cinco siglos. Según referencias, el primer hombre que formuló las regularidades básicas de la fricción seca fue el gran científico italiano Leonardo da Vinci a fines del siglo XV. En 1699, sobre la base de los datos experimentales, el físico francés Guillaume Amontons llegó a las mismas conclusiones hechas por Leonardo da Vinci y formuló la ley de la fricción en su forma clásica: la resistencia al movimiento relativo de los cuerpos sólidos es proporcional a la carga normal y no depende del área de contacto entre los cuerpos; es decir
F = fN
donde: F = resistencia al movimiento relativo de cuerpos sólidos; N = la carga normal en la superficie de fricción; f = el coeficiente de fricción (según Leonardo da Vinci f = 0,25; según Amontons f = 0,30 para todos los cuerpos). En su desarrollo posterior, el estudio de la fricción tomó el camino de la verificación y especificación de los supuestos individuales de esta ley. Entre los científicos cuyos trabajos están dedicados a estos problemas fue el matemático suizo Leonhard Euler. En 1765, dedujo una ecuación que permitía la terminación del esfuerzo de tracción para el movimiento de cuerpos flexibles con fricción a lo largo de una superficie cilíndrica, así como su fuerza de fricción contra el cilindro.
Las obras de muchos investigadores confirmaron básicamente la Ley de Amontons, también se descubrió que los valores del coeficiente de fricción para varios materiales son diferentes y peculiares a pares particulares de materiales de fricción. Al mismo tiempo, hubo una opinión de que la fuerza de fricción depende de la superficie de contacto y el coeficiente de fricción depende de la presión normal. En 1779 C.A. Coulomb expresó la fuerza de fricción como un binomio cuya apariencia contemporánea es:
F = C + f N
El primer término en esta fórmula depende del grado de adhesión de las superficies y el segundo, del valor de la presión sobre ellas. Por tanto, la Ley de Amontons es un caso particular de una regularidad más general revelada por Coulomb. Coulomb ya distinguía la fricción estática y la fricción dinámica (cinética, deslizante). Él creía que la fricción en el momento inicial del deslizamiento de una superficie a lo largo de la otra depende de cuatro razones: 1) la naturaleza de los materiales; 2) la longitud de las superficies; 3) la presión entre las superficies; 4) el tiempo que ha transcurrido desde el momento del contacto de las dos superficies, pero en el caso del deslizamiento relativo, la fricción entre las superficies depende solo de los primeros tres factores.
A pesar de su gran integridad, la fórmula de Coulomb fue olvidada por casi un siglo, y la fórmula de Amontons fue aplicada en cálculos técnicos. Investigaciones posteriores a Coulomb se dirigieron generalmente al establecimiento de la dependencia de la fuerza de fricción sobre la naturaleza de los cuerpos de frotamiento, así como sobre la aplicación de lubricantes. Se descubrió que la fuerza de resistencia al deslizamiento depende de la naturaleza de los cuerpos, el área, el tiempo de contacto y la presión específica. En cuerpos heterogéneos, la fuerza de fricción está determinada por la abrasión del cuerpo más blando, y esta fuerza es mayor para cuerpos más blandos y menor para cuerpos sólidos; la reducción en la fuerza de fricción, cuando se usa un lubricante, depende de la naturaleza del lubricante y no depende de la naturaleza de los cuerpos que se deslizan mutuamente.
Objeciones injustificadas a la teoría de la cuña de tierra de Coulomb
La teoría de Coulomb se cita comúnmente como la teoría de la cuña o prisma
de máximo empuje. Esta definición fue criticada - a finales del siglo XIX -
por Rebhann (1871) y por Winkler (1872) quienes advirtieron a los
especialistas sobre la fiabilidad real de ciertas soluciones a las que se
podría llegar utilizando esta teoría. Como hemos visto anteriormente, entre
todas las cuñas de tierra que ejercen un empuje sobre el muro de contención,
hay uno y solo uno, que produce el empuje máximo. Rebhann y Winkler
consideraron razonable objetar este principio de la siguiente manera:
“Esta afirmación es errónea cuando, debido al principio de acción y
reacción, el empuje es igual a la reacción del muro; sin embargo, este
último debe ser necesariamente independiente de la elección de la cuña de
tierra. Sin embargo, se puede decir, lo que confirma las observaciones de
Coulomb, que la resistencia que ofrece el muro a la acción producida por el
suelo cambia en función de la capacidad de deslizamiento; el valor máximo de
esta resistencia proporciona, por tanto, el límite inferior del
empuje.”
En relación con las contribuciones de Poncelet, Rebhann propuso un
procedimiento simple para determinar la superficie de desprendimiento,
válido incluso si la superficie límite del terreno era curva. Winkler prestó
especial atención al estudio de la influencia de la cohesión y cuestionó,
entre otras cosas, la legitimidad de utilizar los criterios de Rankine en el
diseño de muros de contención.
Es muy probable que tanto Rebhann como Winkler no conocieran directamente
el contenido de las memorias de Coulomb. Esta hipótesis se ve confirmada por
ciertos argumentos expresados por Rebhann en su informe, como la
afirmación perentoria de la “novedad” de los resultados obtenidos por el
científico alemán, también reconocido por Winkler, cuando en realidad
coinciden sustancialmente con los de Coulomb. La única diferencia notable
consiste en el hecho de que Winkler establece el coeficiente de fricción
igual a f (en lugar del 1/n de Coulomb) y deriva el valor del empuje P de la
fórmula
o por simplicidad,
Los argumentos de Coulomb son citados por dos autores alemanes con toda
probabilidad, refiriéndose a una comunicación de Martony de Keszegh
publicada bajo el título de “abreviada” de la teoría de Coulomb: VON MARTONY
DE KOSZEGH, Versuche ueber den Seintendruck der Erde ausgeführt auf höchsten
Befehl … verbunden mit den theoretischen Abhandlungen von Coulomb und
Francais (‘Experimentos sobre la presión de tierra llevados a cabo al más
alto nivel … conectados con los tratados teóricos de Coulomb y Français’),
Wien, 1828.
Aviso sobre las investigaciones de Woltmann, Hagen, Skibinski y Curie
Pasaron más de veinte años antes de que las ideas de Coulomb fueran
recibidas con la atención que merecían en los círculos científicos de la
“mecánica del suelo”. Fuss (1795) por ejemplo, miembro del jurado de un
concurso organizado por la Academia de San Petersburgo sobre el tema del
empuje de tierra, no menciona el trabajo de Coulomb en el informe adjunto al
tema del concurso.
Sin embargo, algunas ideas similares a las de Coulomb parecen haber sido
acogidas favorablemente en Alemania a finales del siglo XVIII. El capitán
von Zach, en un Appendice de la segunda edición del tratado del conde von
Kinsky (1788), expone una teoría muy cercana a la de Coulomb. Informa que
von Kinsky ya había logrado, antes de 1776, los mismos resultados que
Coulomb, resultados que, sin embargo, el autor prefirió abandonar porque no
iban acompañados de una presentación matemática suficientemente
elegante.
El resultado obtenido por Woltmann en 1794 es de mayor interés. Coincide,
en el caso particular de tener cohesión nula, con la de Coulomb, e incluso
la supera en elegancia cuando introduce el ángulo de fricción del suelo en
lugar del coeficiente de fricción estática. Lamentablemente, la falta de
claridad en su presentación disminuye el valor de los resultados que obtuvo,
especialmente si se comparan con los del erudito francés.
La teoría de Woltmann fue retomada a su vez por Hagen (1833), y luego por
Skibinski (1885), quien añadió las siguientes consideraciones: si un muro es
para prevenir deslizamientos de tierra, entonces debe, en cualquier caso,
ejercer un empuje horizontal independiente de la forma de la superficie de
deslizamiento. Si no es posible definir esta superficie, basta con
considerar el peor escenario, es decir, elegir la superficie de
deslizamiento de tal forma que la componente horizontal del empuje sea
máxima. O bien, para evitar que la pared gire alrededor de la esquina
exterior de su base de apoyo, bastará con elegir la superficie de
deslizamiento para la cual el momento de empuje alrededor de este punto sea
máximo. En consonancia con este pensamiento, encontramos los estudios
realizados por Curie en los años 1870-1873.
Obras posteriores sobre la presión de tierra de Coulomb: Prony, Bytelwein, Mayniel, Francais, Audoy y Navier
Al igual que con los otros temas en su memoria en estática, el trabajo de
Coulomb en mecánica de suelos permaneció prácticamente desconocido hasta que
fue utilizado casi cuatro décadas después por el ingeniero y profesor
francés Gaspard de Prony (1755-1839). El enfoque geométrico de Coulomb al
problema de la presión de tierra llevó a otros ingenieros en Francia y
Alemania a desarrollar construcciones geométricas para determinar el empuje
de la presión de tierra. Como era de esperar, la teoría de Coulomb se volvió
dominante cuando se hizo universalmente conocida. Durante los primeros
veinte años del siglo XIX, se desarrolló una gran cantidad de
investigaciones sobre el tema de la presión del suelo y la estática de los
muros de contención. Prony (1802), Eytelwein (1805) y Mayniel (1818)
ampliaron el problema a varios casos especiales que se diferenciaban entre
sí en función de la tipología del revestimiento interior del muro. Su
investigación, a veces expresada sin una forma complicada y no libre de
errores, se basó en el supuesto de que, en ausencia de fricción en el plano
de contacto suelo-muro, el empuje es horizontal y no perpendicular al
revestimiento interno del muro. Prony introdujo una simplificación del
método de Coulomb para ayudar a su aplicación práctica, que es la forma en
que se utiliza hoy en día la fórmula. Partiendo de la ecuación
mediante simples transformaciones trigonométricas sobre la cantidad 1/n =
tan φ, donde φ expresa el ángulo de fricción del suelo, llegó a la conocida
relación que determina el empuje:
donde la cantidad α = (45° - φ/2) identifica la “cuña de máximo empuje” y h
es la altura del muro. El plano ideal que produce el valor máximo del empuje
divide el ángulo α formado por la pared vertical y el plano de pendiente
natural en dos partes iguales. Este resultado permitió a Prony, así como a
muchos autores del siglo XIX, desarrollar las complejas ecuaciones de
Coulomb en un lenguaje matemático accesible a los técnicos.
Prony nació en Chamelet, cerca de Lyon, y entró a l'École des Ponts et
Chaussées en 1776. Después de completar una brillante educación científica,
participó en 1785, a los 28 años, en el diseño y construcción de dos
importantes puentes, y en las obras de rehabilitación del puerto de
Dunkerque junto a Perronet a quien también acompañó en una visita a
Inglaterra. En 1791, como miembro de la comisión francesa sobre el sistema
métrico, estuvo a cargo de los trabajos catastrales necesarios para el
establecimiento del sistema métrico por la Revolución Francesa y, cuando se
adoptó el sistema decimal de división del círculo y exigió la preparación de
nuevas tablas trigonométricas, se le encargó el trabajo. Prony fue uno de
los fundadores y se convirtió en profesor de ciencias matemáticas y el
primer profesor de mecánica en l’École Polytechnique (en 1794) y director de l’Ecole des Ponts et Chausées (en 1798). Sus libros sobre la hidráulica
[“Architecture hydrolique” (1790-1796, 2 vols.)] y sobre la mecánica [
“Leçons de mécanique analytique” (1810)] fueron ampliamente utilizados en
las escuelas de ingeniería de Francia.
Prony escribió no sólo para la profesión de ingeniería sino también
específicamente para los estudiantes de la Ecole polytechnique y la Ecole
des Ponts et Chaussées. En su libro Recherches sur la poussée des terres
(1802) (Figura 1), Prony introdujo el uso de ángulos en lugar de longitudes
(como se usa en la ecuación de Coulomb), simplificó el análisis de la
presión de tierra y presentó un método gráfico de diseño de muros de
contención. Él demostró que el plano de ruptura divide el ángulo entre la
vertical y la línea de pendiente natural, señalando que el plano de presión
máxima de la tierra (Ba en la Figura 2) en realidad bisecta el ángulo entre
la parte posterior del muro y la línea de pendiente natural del suelo. Prony
aplicó la teoría del plano inclinado y la regla del máximo para calcular el
empuje de tierra contra un muro y el ángulo de ruptura correspondiente.
Enseñó sus hallazgos sobre el dimensionamiento de estructuras de contención
de tierra en una clase titulada “Construcciones de obras públicas”. No menos
interesante es su “método gráfico” para dimensionar muros de contención, que
utiliza una tableta gráfica (Figura 1) para resolver los innumerables casos
especiales propios de esta técnica constructiva (en G. Riche de Prony,
Instruction-pratique sur une méthode pour déterminer les dimensions des murs
de revêtement, en se servant de la formule graphique de R. Prony, à Paris,
chez Firmin Didot, 1809).
Fue de esta forma que la mayoría de las memorias de mecánica de Coulomb
entraron en los currículos de estudios de ingeniería en Francia. En dos
artículos publicados para estas escuelas de ingeniería, Prony simplificó el
análisis de Coulomb de presión de tierra. Luego presentó un método gráfico
simple para diseñar muros de contención. Sin embargo, señaló que estaba
empleando la teoría de Coulomb en este trabajo.
 |
Figura
1. Trabajo de Prony |
En 1794, el ingeniero prusiano (alemán) Reinhard Woltmann (1757-1837)
publicó un ensayo sobre la teoría de la presión de tierra utilizando la
misma nomenclatura que la de Coulomb. El trabajo de Woltmann, que incluyó
experimentos realizados en aparatos con muros a gran escala, fue patrocinado
por la Real Academia Científica de Petersburgo. Woltmann nunca citó a
Coulomb, aunque citó el trabajo anterior de Bossut sobre diques (citado por
Coulomb) y empleó la nomenclatura de Coulomb. Woltmann citó obras francesas
publicadas solo antes de 1778. Es probable que no se haya hecho referencia
al trabajo de Coulomb debido a la guerra contemporánea con la Francia
revolucionaria en 1793. Woltmann fue el primero en expresar el empuje de la
presión de tierra en su forma trigonométrica moderna, omitiendo el término
de cohesión del suelo.
Poncelet (1788-1867) y otros desarrollaron posteriormente métodos gráficos
de solución para el problema de la presión de tierra. Poncelet en su
revisión histórica de varias teorías de arcos (anteriormente mencionado)
comenta: “La memoria de Coulomb contienen en pocas páginas tantas cosas que
durante cuarenta años la atención de ingenieros y científicos no se fijó en
ninguna de ellas”. En 1857 Rankine publicó su teoría del esfuerzo conjugado
de la presión del suelo. Por un tiempo, esta suplantó el método de Coulomb,
pero las autoridades modernas están de acuerdo en que la teoría de la cuña
de Coulomb no solo es más simple que la de Rankine, sino que también explica
con mayor precisión los datos observados.
En el diseño de los muros de contención, los ingenieros continuaron
utilizando métodos basados en la suposición de Coulomb de que el
deslizamiento de arena ocurre a lo largo de un plano inclinado, y el avance
principal radica en el desarrollo de métodos puramente gráficos de análisis.
Se puede encontrar una bibliografía completa para este campo en los
artículos de Felix Auerbach y Felix Hulsenkamp, “Handbuch der physikalischen
und technischen Mechanik (Manual de Mecánica física y técnica)”, vol 42,
1931. G. Rebhann propuso un método muy útil de este tipo (G. Rebhann,
“Theorie des Erddruckes und der Futtermauern mit besonderer Rucksicht auf
das Bauwesen (‘Teoría de la presión de la tierra y los muros de
revestimiento con especial consideración en la construcción’)”, Viena,
1871).
Resumen de los principales aspectos sobre la cuña de tierra de Coulomb
Los hallazgos básicos de Coulomb se resumen de la siguiente manera:
Considerando la estática de una cuña de suelo como CBa (Figura 2), obtuvo
una expresión para la fuerza horizontal A, que mantendría la cuña en
equilibrio cuando se movilizara toda la resistencia al corte a lo largo de
Ba. Derivó su expresión para la fuerza A, igualó el resultado a cero y
finalmente obtuvo la expresión particular para la “presión activa de tierra”
en la parte posterior de un muro vertical (sin fricción de muro y sin carga
de sobrecarga) como se muestra en la ecuación
donde:
h = Altura de la cuña suelo
a, b = Funciones de n
que se puede reducir a la forma trigonométrica moderna como se muestra en
la siguiente ecuación
donde:
γ = Peso unitario del suelo
c = Cohesión del suelo
Coulomb dio ejemplos que muestran que la expresión produjo parámetros de
diseño para muros de acuerdo con la práctica aceptada en ese momento.
Mostró que la fuerza A podría aumentar a un valor A’, y que el equilibrio
se mantendría hasta que se exceda este valor cuando la cuña se mueva hacia
arriba en el plano Ba. La fuerza de Coulomb A’, es lo que ahora se llama
presión pasiva de tierra.
Se dio cuenta de que la superficie de ruptura es curva, pero asumió una
línea de deslizamiento recta. Afirmó que la cohesión no tiene influencia en
la posición del plano de falla y que para un material puramente cohesivo el
plano está inclinado a 45°.
El caso de sobrecarga del muro (ver Figura 2) se resolvió junto con el caso
de la fricción del muro. Se dio cuenta de que la fricción del muro reduce la
presión total y aumenta la estabilidad del muro. Sin embargo, no consideró
los muros con respaldos inclinados o rellenos inclinados. Coulomb dedujo la
regla de diseño como se muestra en la siguiente ecuación:
donde:
w = Espesor del muro
Por lo tanto, de acuerdo con la teoría de Coulomb, un muro de 1 metro de
espesor soportaría un relleno horizontal de 7 metros de altura. Esta regla
de diseño no es un dimensionamiento conservador para un muro en comparación
con las reglas modernas, incluso con un muro de inclinación en el
intradós.
También discutió las precauciones al dimensionar un muro inclinado en el
intradós sin abordar los problemas prácticos de la estructura del suelo
(fricción del suelo con la mampostería y presión hidrostática del agua de
filtración, efecto del suelo húmedo sobre la fricción, acción de las
heladas). Afirmó que era seguro construir un muro con una inclinación en el
intradós de 1:6 y un espesor en la corona igual a 1/7 de la altura.
 |
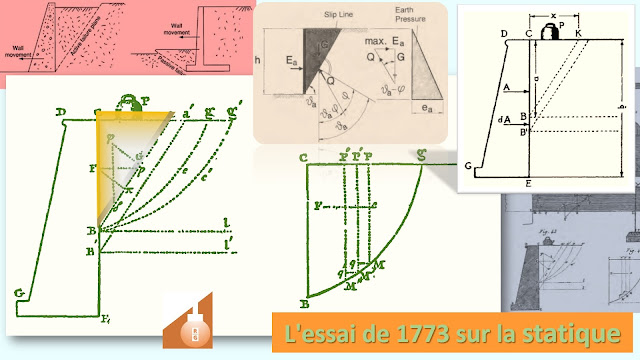
Figura 2. Extracto de
la Memoria sobre Estática de 1773 |
El criterio de rotura
El término rotura o falla (o cedencia, yield (en inglés)) se refiere al
inicio de un comportamiento inelástico. Se debe suponer un elemento de
material que se somete a un sistema de esfuerzos de magnitud que aumenta
gradualmente. La deformación inicial del elemento es totalmente elástica y
la forma original del elemento se recupera en la descarga completa. Para
ciertas combinaciones críticas de los esfuerzos aplicados, la deformación
plástica aparece primero en el elemento. Una ley que define el límite del
comportamiento elástico bajo cualquier combinación posible de esfuerzos se
denomina criterio de falla (o criterio de rotura o de fluencia). La ley se
aplica no solo al cargar directamente desde el estado rígido, sino también
al recargar de un elemento descargado de un estado plástico anterior. Al
desarrollar una teoría matemática, es necesario tener en cuenta una serie de
idealizaciones desde el principio. En primer lugar, se supone que las
condiciones de carga son tales que se pueden despreciar todas las tasas de
deformación y los efectos térmicos. En segundo lugar, se ignora el bucle de
histéresis, que surge de la falta de uniformidad en la escala del
microscopio. Finalmente, se asume que el material es isótropo, por lo que
sus propiedades en cada punto son las mismas en todas las direcciones.
Existe una simplificación útil e inmediata que resulta del hecho
experimental de que la fluencia prácticamente no se ve afectada por una
tensión o compresión hidrostática uniforme. Los efectos de estas
restricciones sobre la naturaleza del criterio de rotura se examinarán
primero en términos geométricos.
En parte por simplicidad en la práctica y en parte debido al desarrollo
histórico de la mecánica de los sólidos deformables, los problemas de la
mecánica de suelos a menudo se dividen en dos grupos distintos: los
problemas de estabilidad y los problemas de elasticidad. Luego se tratan de
dos maneras separadas y no relacionadas. Los problemas de estabilidad se
refieren a las condiciones de rotura final de una masa de suelo. Los
problemas de presión del suelo, capacidad de carga y estabilidad de taludes
se consideran con mayor frecuencia en esta categoría.
La característica más importante de tales problemas es la determinación de
las cargas que provocarán la falla de la masa del suelo. Las soluciones a
estos problemas se obtienen a menudo utilizando la teoría de la plasticidad
perfecta. Los problemas de elasticidad, por otro lado, se relacionan con el
esfuerzo o la deformación del suelo cuando no se trata de una falla del
suelo. Los esfuerzos en puntos de una masa de suelo debajo de una zapata o
detrás de un muro de contención, las deformaciones alrededor de túneles o
excavaciones y todos los problemas de asentamiento pertenecen a esta
categoría. Las soluciones a estos problemas se obtienen a menudo utilizando
la teoría de la elasticidad lineal.
La teoría de la elasticidad lineal se basa en la ley de Hooke que establece
una relación lineal entre esfuerzo y deformación. Aunque Hooke introdujo por
primera vez el concepto de elasticidad lineal en la década de 1660, no fue
hasta 1807 cuando Young reconoció el cizallamiento como una deformación
elástica. La elasticidad lineal tridimensional en sí misma solo se formalizó
realmente en la década de 1820 (Navier, Cauchy y otros) al mismo tiempo que
el concepto de tensor de esfuerzos. La teoría de la plasticidad perfecta
tiene en cuenta el hecho de que el suelo real exhibe el comportamiento
mecánico estipulado por la ley de Hooke solo mientras la intensidad del
esfuerzo sea suficientemente pequeña. Cuando la intensidad del esfuerzo
alcanza por primera vez un cierto valor crítico, que se denomina valor de
rotura (o de fluencia o de falla), el suelo abandona el rango elástico y
entra en el rango de flujo plástico, lo que indica una deformación continua
en un estado de esfuerzo constante. Para mantener el flujo plástico, la
intensidad del esfuerzo debe estar en el valor de rotura, pero nunca puede
exceder este valor. Tan pronto como la intensidad del esfuerzo desciende por
debajo de este valor, cualquier cambio de deformación es de naturaleza
puramente elástica.
En el intermedio entre los problemas de elasticidad y los problemas de
estabilidad mencionados anteriormente están los problemas conocidos como de
falla progresiva. Los problemas de falla progresiva tratan con la transición
elástica-plástica del estado elástico lineal inicial al estado de falla
final del suelo por flujo plástico.
Coulomb estableció el primer criterio de falla útil para el suelo en 1773.
Constituye una de las piedras angulares de la comprensión de la forma en que
se comportan los suelos.
Hipótesis de plástico perfectamente elástico
La Figura 3 muestra un diagrama de esfuerzo-deformación típico para suelos,
asociado con una prueba de corte simple o una prueba de compresión triaxial.
El comportamiento de esfuerzo-deformación de la mayoría de los suelos reales
se caracteriza por una porción lineal inicial y un esfuerzo pico (máximo) o
de rotura seguido de un ablandamiento a un esfuerzo residual. En el análisis
de límites, es necesario ignorar la característica de ablandamiento por
deformación (o ablandamiento por trabajo) del diagrama de
esfuerzo-deformación y tomar el diagrama de esfuerzo-deformación que consta
de dos líneas rectas, como se muestra con las líneas discontinuas en la
Figura 3. Un material hipotético que exhibe esta propiedad de flujo plástico
continuo bajo esfuerzo constante se denomina material idealmente plástico o
perfectamente plástico.
 |
Figura 3. Relación esfuerzo-deformación para suelos
ideales y reales |
Cabe señalar que el nivel de esfuerzo de falla (o de fluencia) utilizado en
aplicaciones de análisis de límites donde se asume una plasticidad perfecta
puede elegirse para representar el esfuerzo promedio en un rango apropiado
de deformación. Por tanto, la validez de la hipótesis de plasticidad
perfecta puede ser más amplia de lo que podría parecer posible a primera
vista. La elección del nivel del límite elástico no es absoluta, sino que
está determinada por las características más significativas del problema a
resolver. Para problemas de estabilidad, esta suposición puede ser más
justificable que para otros problemas en la mecánica de suelos. Como
ilustración, la falla por cortante en el suelo debajo de la zapata que se
muestra en la Figura 4 es un fenómeno de falla progresiva a niveles de
esfuerzo bastante variables. En consecuencia, cuando la superficie de
deslizamiento potencial abcde alcanza los puntos a y e, simplemente
movilizando el esfuerzo cortante pico en estos dos puntos, la resistencia
del suelo al comienzo de la superficie de deslizamiento, punto c, debe estar
muy por debajo del pico y cerca del esfuerzo de cortante residual.
 |
Figura 4. Análisis de límites y soluciones de línea de
deslizamiento |
En el instante del colapso, la resistencia máxima al cortante disponible
sobre esta superficie debe tener un valor en algún lugar entre el esfuerzo
máximo y el esfuerzo residual. Un mayor desplazamiento de la zapata
provocaría que este esfuerzo cortante promedio cayera hacia el valor
residual.
En todos los problemas de estabilidad, el esfuerzo cortante promedio máximo
movilizado sobre toda la superficie de falla en un suelo real será menor que
el valor pico y mayor que el valor residual, estando su posición relativa
entre estos dos límites determinada tanto por las propiedades del suelo y
por la geometría y las tensiones de contorno en el problema a
analizar.
Resistencia al corte del suelo - Ley de fricción y cohesión o Criterio de Rotura de Coulomb
Para muchas clases de material, solo se debe especificar un valor de
cortante o de resistencia al corte para diseñar una estructura fabricada con
esa sustancia. Los metales, por ejemplo, se formulan y fabrican con una
determinada especificación de resistencia a la tracción o esfuerzo cortante
máximo, y una de estas cantidades es suficiente para analizar la resistencia
y el factor de seguridad de un componente estructural. Si, a modo de
ilustración, un grado particular de acero al carbono tiene un límite
elástico a la tracción de 300 MPa (y por lo tanto un límite elástico al
corte de 150 Mpa), este valor permanecerá sin cambios sin importar el nivel
de presión que se aplique sobre la superficie de corte dentro del
material.
Los suelos en general no entran en esta categoría de material. Al estar
compuestos de partículas minerales que no interactúan mecánicamente como lo
hacen los átomos metálicos, no se puede dar un valor único de esfuerzo
cortante máximo (o resistencia al corte). Coulomb en su Memoria sobre
Estática de 1773 proporcionó la primera descripción completa de la
resistencia al corte del suelo. Afirmó que el límite de la resistencia al
corte se compone de dos componentes, a saber, la cohesión y la fricción. La
cohesión es la parte de la resistencia que se puede medir mediante la
ruptura directa de dos partes de un cuerpo en tensión. En otras palabras,
ese es el componente de la resistencia al corte que no depende de la presión
perpendicular sobre la superficie de ruptura del material. Coulomb midió los
valores de cohesión mediante ensayos de tracción destructivos en roca de
cantera del área de Burdeos (Figura 5), Francia, como se muestra en su
figura 1 (Figura 6), así como en ladrillos de diferentes edades.
 |
Figura 5. Cantera de piedra caliza de Frontenac o de Bordeaux |
 |
| Figura 6. Reproducción de las ilustraciones originales de Coulomb (1776) que muestran (1) una prueba de resistencia a la tracción en roca blanca de cantera, (2 y 3) pruebas de corte y flexión en vigas de roca, (4) la adición de vectores de fuerza, (5) una prueba de compresión en un pilar de mampostería y el ángulo del plano de falla en un material friccionante, (6) esfuerzos de flexión de la viga y (7 y 8) falla activa del suelo detrás de un muro de contención con una superficie de falla del suelo curva y en línea recta aproximadas |
La fricción, por otro lado, es un proceso en el que la resistencia al corte
depende de la presión perpendicular sobre la superficie deslizante. Coulomb
citó a su compatriota Amontons como prueba de que muchos materiales
demuestran un comportamiento de fricción lineal, es decir, la resistencia al
corte es proporcional a la presión normal en un plano particular dentro de
un cuerpo material. Coulomb usó la figura 5 (Figura 6) para demostrar que el
ángulo del plano de falla por cortante en un material de fricción es mayor
que 45° más la mitad del ángulo de fricción interna, mientras que el plano
de ruptura se observa con una inclinación de 45° en materiales puramente
cohesivos. Aplicando estos conceptos de resistencia del suelo a la mecánica
del movimiento de tierras, Coulomb calculó planos de falla curvos en el
suelo detrás de muros de contención como se muestra esquemáticamente en sus
figuras 7 y 8 (Figura 6).
Los problemas de la mecánica de suelos, como los relacionados con la
estabilidad de los taludes, la limitación de la presión (empuje) sobre los
muros de contención y la capacidad de carga de las losas de cimentación,
suelen tratarse como problemas de plasticidad. La falla de los suelos
granulares ocurre por simple deslizamiento y puede describirse mediante un
criterio de rotura en el que la parte hidrostática del esfuerzo juega un
papel importante. Se supone que la magnitud del esfuerzo cortante que actúa
sobre cualquier plano de deslizamiento a través de una masa de suelo
isotrópico varía linealmente con el esfuerzo normal a través del plano. Esta
condición, propuesta originalmente por Coulomb (1773), se denomina en la
terminología moderna de resistencia de materiales, ley de Coulomb de
resistencia al corte del suelo y se puede expresar de la siguiente
manera.
donde:
s = resistencia al corte del suelo (esfuerzo cortante máximo) (Figura
7);
c = cohesión, la parte de la resistencia independiente de la presión
normal;
σn = esfuerzo normal al plano de deslizamiento (Figura 7);
𝜙 = ángulo de fricción interna del material.
En la ecuación, la tangente del ángulo de fricción interna, tan 𝜙, es el
coeficiente de fricción comúnmente utilizado al calcular la resistencia al
deslizamiento de un cuerpo de material sobre otro. En esta aplicación, el
coeficiente es el de la resistencia a la fricción en una superficie interna,
y es la constante del aumento proporcional de la resistencia al corte con el
aumento de la presión normal sobre la superficie (Figura 7).
 |
Figura 7. Esfuerzos perpendiculares (normales) y
paralelos (cortantes) en la superficie de deslizamiento interna de un bloque de
suelo que falla |
Es importante conocer el comportamiento del suelo ante un estado de
esfuerzos complejo. En particular, es necesario tener una idea de las
condiciones que caracterizan el cambio del material de un estado elástico a
un estado de fluencia o flujo (la línea horizontal ab en la Figura 3). Aquí
surge la pregunta de una posible forma de la condición que caracteriza la
transición de un suelo de un estado elástico a un estado de flujo plástico
con un estado de esfuerzos complejo. Esta condición, satisfecha en el estado
de fluencia, se denomina criterio de rotura o de fluencia (condición de
plasticidad perfecta).
Generalmente se asume que el flujo plástico ocurre cuando, en cualquier
plano en cualquier punto de una masa de suelo, el esfuerzo cortante alcanza
una cantidad que depende linealmente del esfuerzo de cohesión y el esfuerzo
normal, siempre que sea un esfuerzo de compresión. Las constantes de
cohesión c y cohesión 𝜙 pueden considerarse simplemente como parámetros que
caracterizan la resistencia total del medio del suelo al
cizallamiento.
Es habitual llamar a un medio de suelo en el que no hay cohesión (c = 0) un
suelo sin cohesión, y uno en el que no hay fricción interna (𝜙 = 0) un suelo
puramente (o idealmente) cohesivo.
El legado del ensayo de Coulomb
La aparición de la mecánica de suelos como ciencia de la ingeniería a
menudo se asocia con la Memoria sobre Estática de Coulomb, presentada a la
Academia de Ciencias de Francia en 1773 después de que Coulomb regresara de
su período de ocho años en Martinica como teniente en el cuerpo de
ingenieros militares franceses. Este Ensayo estuvo dedicado a varios
problemas con los que se había encontrado al construir el “Fuerte Borbón”:
estabilidad de pilares, arcos y bóvedas, cálculo de la presión del suelo en
muros de contención, etc. La primera idea rectora de la lógica de Coulomb al
abordar estos problemas es hacer una clara distinción entre las fuerzas
activas, que son las cargas prescritas que actúan sobre la estructura en
consideración, y las características de resistencia del material, que
establecen los límites a las fuerzas de “coherencia” que se pueden movilizar
(Figura 8).
 |
Figura 8. Definición de fricción y cohesión en el
‘Essai’ de Coulomb |
La segunda idea rectora es que las fuerzas de resistencia se ejercen
localmente a lo largo de una supuesta superficie de falla, anticipando, en
cierta medida, el concepto de vector de esfuerzos que se introducirá unos 50
años después. En el caso simple de una columna de piedra bajo una carga de
compresión (Figura 5 de la Plancha 1 de Coulomb en la Figura 6), Coulomb
explica los principios del análisis: la fuerza activa sobre la supuesta
superficie de fractura debe ser equilibrada por la fuerza de “coherencia”;
la superficie de la fractura se determinará mediante un proceso de
minimización.
Sobre la base del mismo principio, el análisis de estabilidad de Coulomb de
un muro de contención es un hito fundamental para la teoría del diseño a la
rotura. Coulomb comienza con el célebre razonamiento de la “cuña de Coulomb”
(Figuras 2 y 6), donde asume que la superficie de falla es plana y
establece una condición para la estabilidad de que las fuerzas activas en la
supuesta superficie de fractura Ba deben estar equilibradas por la fuerza de
“coherencia”, de las cuales deriva, a través de procesos de minimización y
maximización, dos límites para la fuerza horizontal que se puede aplicar a
CB para que el muro sea estable. Debido a su simplicidad, este razonamiento
se presenta a menudo como el análisis de Coulomb de la estabilidad de un
muro de contención. De hecho, Coulomb, después de mostrar cómo se podría
tener en cuenta la fricción a lo largo del muro, afirma que, para ser
completo, el análisis debe buscar la curva que produce la mayor presión
sobre CB y esboza el proceso para esta determinación.
La Mémoire de Coulomb fue el origen de muchos métodos utilizados por los
ingenieros para el análisis de estabilidad de varios tipos de estructuras.
En el caso de las bóvedas de mampostería, las obras de Méry y Durand-Claye
han sido ampliamente estudiadas por Heyman y Delbecq: es interesante notar
que a menudo combinaban el razonamiento original de Coulomb con argumentos
elásticos, perdiendo así su significado teórico original sin ningún daño
desde el punto de vista práctico.
La mecánica de suelos, que a veces se considera que tiene su origen mismo
en la Memoria de Coulomb, exhibe numerosos métodos claramente relacionados
con ella para el análisis de estabilidad de taludes, muros de contención,
rellenos y presas de tierra o para el cálculo de la capacidad portante de
las cimentaciones superficiales, incluyendo los métodos de equilibrio límite
y los métodos de línea de deslizamiento, que también se aplicaron para
resolver problemas de conformado de metales. Los métodos de elementos
finitos también se han desarrollado y utilizado ampliamente dentro de este
marco para aplicaciones a la mecánica de suelos y a algunos problemas
relacionados. Otro campo de aplicación es la capacidad portante de placas
metálicas y losas de concreto reforzado a través de la teoría de las
bisagras de rotura desarrollada por Johansen, Save, Massonnet y otros. Chen,
Drucker y sus coautores han prestado considerable atención a la aplicación
de los teoremas del análisis de límites para la determinación de la
capacidad portante de bloques de concreto y concreto reforzado con fibra.
Más recientemente, se ha aplicado a la determinación de la resistencia de
fibras compuestas largas a partir del conocimiento de las resistencias de
los componentes mediante un proceso de homogeneización que conduce a la
definición y determinación de un criterio de falla homogeneizado.
Mecánica de suelos y mecánica del continuo como legado del ‘Essai’
Incluso la inspección más casual de cualquier suelo real muestra claramente
el carácter aleatorio, particulado y desordenado que se asocia con los
materiales naturales de origen geológico. El suelo será una mezcla de
partículas de diferente contenido mineral (y posiblemente orgánico), y el
espacio poroso entre las partículas estará ocupado por agua, aire o ambos.
Hay muchas virtudes importantes relacionadas con este aspecto de un suelo,
entre ellas su uso como medio agrícola; pero, cuando nos acercamos al suelo
en un contexto de ingeniería, a menudo será deseable pasar por alto su
carácter particulado. Existen teorías modernas que modelan directamente el
comportamiento de las partículas, pero en casi todas las aplicaciones de
ingeniería se idealiza el suelo como un continuo: un cuerpo que puede
subdividirse indefinidamente sin alterar su carácter.
El tratamiento del suelo como un continuo tiene sus raíces en el siglo
XVIII cuando el interés por la mecánica de suelos comenzó en serio. Charles
Augustin Coulomb implicó claramente la descripción del continuo del suelo
con fines de ingeniería en su Memoria sobre Estática de 1773. Desde
entonces, casi todas las teorías de ingeniería del comportamiento del suelo
de interés práctico han dependido del supuesto del continuo. Conforme a
Coulomb, la resistencia del suelo se compone de dos elementos: cohesión y
fricción. Como se trata de arena, la cohesión será cero y, por tanto, la
resistencia a la fricción viene dada por el producto del esfuerzo normal
efectivo promedio que actúa sobre la superficie multiplicado por el
coeficiente de fricción del suelo. En geomecánica se representa el
coeficiente de fricción por la tangente de un ángulo ϕ llamado ángulo de
fricción interna.
Referencias
Benvenuto, E. (1991). An Introduction to the History of Structural
Mechanics. Part I: Statics and Resistance of Solids. Springer.
Benvenuto, E. (1991). An Introduction to the History of Structural
Mechanics. Part II: Vaulted Structures and Elastic Systems. Springer.
Bordes, J.L. (2000). Regard sur le passé de la géotechnique. Revue
Française de Géotechnique. 2e trimestre 2000. Pag. 13-26.
Chakrabarty, J. (2006). Theory of Plasticity. Elsevier. Third
edition.
Chen, W-F. (1975). Limit Analysis and Soil Plasticity. Elsevier.
Coduto, D. (2001). Foundation Design: Principles and Practices.
Coduto, D. P., Yeung, R. M., Kitch, W. A. (2011). Geotechnical Engineering:
Principles and Practices, 2nd Edition. Pearson Education, Inc.
Coulomb, C. A. (1776). “Essai sur une Application des Règles de Maximis et
Minimis á quelques Problemes de Statique, relatifs à l’Architecture”. Mem.
Div. Sav. Académie des Sciences.
Cuizon, S. A. (2015). Introduction to Soil Mechanics. Technological
University of the Philippines.
Das, B.M. (2009). Principles of Geotechnical Engineering. 7th Edition. Pgs.
4-7.
Davis, R. y Selvadurai, A. (2002). Plasticidad y geomecánica. Prensa de la
Universidad de Cambridge.
Gillmor, C. S. (1968). “Charles Augustin Coulomb: Physics and Engineering
in Eighteenth-Century France,” PhD dissertation, University of
Princeton.
Gillmor, C. S. (1971). Coulomb and the Evolution of Physics and Engineering
in Eighteenth-Century France, Princeton University Press, Princeton, New
Jersey, U.S.A.
de Boer, R. (2000). Theory of Porous Media: Highlights in Historical
Development and Current State. Springer. Verlag. Berlin. Heidelberg. New
York.
Heyman, J. (1972). Coulomb's Memoirs on Statics: An Essay in the History of
Civil Engineering. Cambridge, U.K.
Heyman, J. (1998). Structural Analysis. A Historical Approach. Cambridge
University Press.
Holtz, Robert D., Kovacs, William D. & Sheahan, Thomas C. An
Introduction to Geotechnical Engineering. 2nd Edition. Prentice Hall.
2011.
Kerisel, J. (1993). Retaining Structures: Proceedings of the Conference
Retaining Structures. Editor C. R. I. Clayton, Institution of Civil
Engineers (Great Britain). Thomas Telford, London.
McKyes, E. (1989). Agricultural Engineering Soil Mechanics. Elsevier.
Punmia, B.C., Jain, A.K. (2006). Soil Mechanics and Foundations. 17th Ed.
Laxmi Publications Ltd.
Radelet-de Grave, P. & Benvenuto, E. eds. 1995. Entre Mecanique et
Architecture - Between Mechanics and Architecture. Basel; Boston; Berlin:
Birkhäuser
Salençon, J. (2013). Yield Design. Wiley.
Skempton, A. W. (1979). Landmarks in early soil mechanics. Jalons dans les
premiers siécles de la mécanique des sols. Proc. 7th Eur. Conf. Soil Mech.,
Brighton, 1979, 5, 1-26.
Skempton, A. W. (1985). A History of Soil Properties, 1717-1927. Golden
Jubilee Volume. Proceedings of the Eleventh International Conference on Soil
Mechanics and Foundation Engineering, San Francisco, 12-16 august
1985.
Timoshenko, S. (1953). A History of Strength of Materials. With a brief
account of the history of theory of elasticity and theory of structures, New
York: McGraw-Hill Book Company.
Vilde, A., Sevostjanovs, G., Nowak, J. (2007). Theories of Friction and
their Applicability to Soil. TEKA Kom. Mot. Energ. Roln. OL PAN, 2007, 7, 250–260.
Cita
Osorio, S. (2021). L'essai de 1773 sur la statique - 4a parte. Relatos de la Geotecnia. Blogger.com. geotecnia-sor2.blogspot.com. https://geotecnia-sor2.blogspot.com/2021/10/lessai-de-1773-sur-la-statique-4a-parte.html
Relatos de la Geotecnia
+ Apuntes de Geotecnia con Énfasis en Laderas
Ir a:
1 - Martinique, Antilles - France Février 1764 (Martinica, Antillas - Francia , febrero de 1764)
2 - Angoulême, province d'Angoumois - France 14 juin 1736 (Angoulême, provincia de Angumois - Francia, 14 de junio de 1736)
3 - Mézières, département des Ardennes - France 11 février 1760 (Mézières, departamento de Ardennes - Francia, 11 de febrero de 1760)
4 - Paris - France 10 mars 1773 (París - Francia, 10 de marzo de 1773)
5 - L'essai de 1773 sur la statique - 1a Parte (La Memoria sobre Estática de 1773 - 1a Parte)
6 - L'essai de 1773 sur la statique - 2a Parte (La Memoria sobre Estática de 1773 - 2a Parte)
7 - L'essai de 1773 sur la statique - 3a Parte (La Memoria sobre Estática de 1773 - 3a Parte)
9 - L'essai de 1773 sur la statique - 5a Parte (La Memoria sobre Estática de 1773 - 5a Parte)
10 - L'essai de 1773 sur la statique - 6a Parte (La Memoria sobre Estática de 1773 - 6a Parte)
11 - L'essai de 1773 sur la statique - 7a Parte (La Memoria sobre Estática de 1773 - 7a Parte)
12 - L'essai de 1773 sur la statique - 8a parte (La Memoria sobre Estática de 1773 - 8a Parte)
13 - La vie de Coulomb après l’Essai de 1773 (La vida de Coulomb posterior al 'Essai' de 1773)Apéndice A - Fuerte Bourbon (1765-1772)
Apéndice C - La Estática de las Siete Máquinas Simples
Apéndice D - La Statique (La Estática)
Apéndice E - Mécanique Classique (Mecánica Clásica)
Apéndice F - De la résistance des matériaux (De la Resistencia de Materiales)
Diseño: PatoMOP
2021
Comentarios
Publicar un comentario
Bienvenidos, agradezco sus comentarios ...