L'essai de 1773 sur la statique - 2a parte
Por: Santiago Osorio R.
Segunda parte de la quinta entrega de la serie 'DU PLAN INCLINÉ À LA THÉORIE DU COIN DES TERRES' (Del plano inclinado a la teoría de la cuña de suelo), una visión detallada del aporte de Charles Augustin Coulomb a la consolidación de
la teoría clásica de la mecánica de suelos. Octubre 7 de 2021.
Al examinar tratados clásicos de la ingeniería como La science des ingénieurs de Bélidor (1729), o el Traité de stéréotomie de Amédée Frézier (1760), se encuentra que los principales temas que ocupaban a los ingenieros de la época, son la resistencia de los materiales de albañilería (mampostería), el diseño de muros de contención y el diseño de arcos. Estos son precisamente los problemas que Coulomb abordó en su memoria de estática de 1773, en la que estaba haciendo dos cosas:
1) Introducir el uso del cálculo variacional en la teoría de la ingeniería, involucrando un problema matemático consistente en buscar máximos y mínimos (o más generalmente extremos relativos de funcionales continuos definidos sobre algún espacio funcional), propuesto inicialmente por Leonhard Euler (1707-1783). La teoría de máximos y mínimos de Coulomb se deriva del equilibrio estático.
2) Plantear los principales problemas de ingeniería civil para considerar las complejidades de la naturaleza. Los problemas de estática de Coulomb pueden parecer desconectados entre sí, pero estaban en el corazón de la ingeniería del siglo XVIII.
En suMemoria sobre Estática, Coulomb redescubre y amplía los resultados de la obra de 1713 sobre geometría analítica tridimensional de Antoine Parent (1666-1716), reconociendo en las “reglas del máximo y mínimo” un nuevo argumento para retornar la teoría “a una armonía y un orden que satisfagan el espíritu”. En 1713 derivó la fórmula correcta para la flexión de vigas en voladizo. Asumió correctamente un eje central neutro y una distribución de tensión lineal desde la tracción en la cara superior hasta la compresión igual y opuesta en la parte inferior, obteniendo así un módulo de sección elástico correcto del área de la sección transversal multiplicada por la profundidad de la sección dividida por seis. Desafortunadamente, el trabajo de Parent tuvo poco impacto, y pasaron muchos años más antes de que los principios científicos se aplicaran regularmente al análisis de la resistencia de las vigas a la flexión.
En la primera mitad del siglo XVIII, el ingeniero francés Pierre Couplet
(1670-1744) en Seconde partie de l’examen de la poussée des voûtes
('Segunda parte del examen de empuje de la bóveda', 1732), basado en el
trabajo del matemático francés Philippe de La Hire (1640-1718), presentó una
solución notablemente completa al problema de calcular el espesor mínimo de
un arco de mampostería semicircular con radio de espesor medio, R y espesor,
t, capaz de soportar su propio peso. Su trabajo presenta de la manera más
lúcida los dos conceptos clave necesarios en el análisis de equilibrio
límite de arcos de mampostería que no soportan tensión: (a) la línea de
empuje límite; y (b) el mecanismo de colapso inminente. Couplet (1730)
reconoció que cuando el grosor del arco semicircular es suficientemente
pequeño, el arco desarrolla un mecanismo simétrico de cinco bisagras. Las
cinco bisagras del mecanismo simétrico se desarrollan en el extradós de la
corona del arco, en el extradós del ‘springer’ (la piedra más baja en un
arco, donde comienza la curva) y en una ubicación desconocida a lo largo del
intradós del arco (Figura 1).
Para determinar la posición de la bisagra intradós, Couplet necesitaba una
tercera ecuación distinta de las dos ecuaciones ofrecidas por el momento de
equilibrio. En el estado de equilibrio límite del arco, esta tercera
ecuación se ofrece a partir de la aplicación del principio de energía
potencial estacionaria que maduró cuando Lagrange en 1788, desarrolló su
cálculo variacional unos 50 años después del trabajo de Couplet. Pierre
Couplet pasa por alto este impasse simplemente asumiendo (quizás después de
haber sido influenciado por Bélidor en su tratado La science des ingénieurs
de 1729, que la ubicación de la ruptura que forma la bisagra intradós está a
45°. De esta forma, Couplet fuerza la selección del mecanismo de falla; por
lo tanto, su solución para el espesor mínimo, t/R
= 0.101, no es conservadora, dado que un mecanismo vecino podría haberse
desarrollado con un espesor mayor. Sin embargo, en ausencia de cálculo
variacional en 1730, Pierre Couplet hizo todo lo posible para estimar el
grosor mínimo de un arco semicircular.
|
|
|
Siguiendo el trabajo pionero de Pierre Couplet y durante los siglos XVIII y
XIX, existe una creciente necesidad en Europa de puentes y acueductos de
mampostería. En la segunda mitad del siglo XVIII C.A. Coulomb se ve motivado
por la necesidad de desarrollar una teoría general sobre la estabilidad de
las estructuras de mampostería y en 1773 presenta su teoría seminal de
máximos y mínimos. Coulomb sin hacer referencia al trabajo de su compatriota
Couplet, concluye que el mecanismo de falla más crítico de un arco de
mampostería es el mecanismo de bisagra (más que un mecanismo deslizante) y
le preocupa su identificación. Tomando una sección arbitraria del arco,
Coulomb (1773) calcula los límites máximo y mínimo de la fuerza de empuje
horizontal en la corona que se necesita para mantener la estructura en
equilibrio, del empuje horizontal máximo y la maximización del empuje
horizontal mínimo que conduce a la posición de bisagra interna más crítica.
La principal contribución de C.A. Coulomb es que reconoce la necesidad de
examinar mecanismos vecinos admisibles en la mecánica estructural y todo su
razonamiento está en línea con la teoría recientemente desarrollada en
matemáticas conocida como cálculo de variación.
Cálculo básico y su aplicación al análisis de estructuras
Por la época en que Gian Lorenzo Bernini estaba dando los toques finales a
la plaza de San Pedro en Roma y Christopher Wren estaba comenzando a
construir la nueva Catedral de San Pablo, Newton y Leibniz desarrollaron el
cálculo, una nueva matemática poderosa y ampliamente aplicable. Las
circunstancias que rodearon a estos dos genios no podrían haber sido más
diferentes.
Isaac Newton (1642-1727), un estudiante universitario inglés de unos veinte
años, regresó a la granja familiar cuando la peste negra cerró la
Universidad de Cambridge. Con conocimientos extraordinarios y gran capacidad
de concentración, trabajó allí por su cuenta en los años 1665 y 1666. En
este corto período de tiempo, formuló las leyes básicas de la física del
movimiento, se dio cuenta de que aplicaban en todo el universo, y desarrolló
el cálculo, las matemáticas que le permitieron extraer la información que le
proporcionaban las leyes básicas. Luego demostró que las trayectorias
parabólicas que describió Galileo y las órbitas elípticas de los planetas
que Kepler había documentado son mucho más que realidades observadas: son
consecuencias matemáticas de las leyes fundamentales del movimiento. Newton
retrasó la versión publicada -el
Principia Mathematica- de esta síntesis hasta 1687 porque
publicaciones anteriores lo habían envuelto en largas disputas con
científicos contemporáneos. El Principia Mathematica es (junto con
El Origen de las Especies de Darwin) el volumen científico más
importante jamás escrito.
El otro genio fue Wilhelm Gottfried Leibniz (1616-1716), un alemán que tenía
poco más de veinte años cuando estaba en una misión diplomática en París en
nombre de su patrón, el duque de un estado germánico. Inspirado por algunos
de los intelectuales de esta ciudad, desarrolló el cálculo de forma
independiente entre 1673 y 1676. El tratamiento que hizo Leibniz del tema
fue más algebraico y notoriamente más claro que el enfoque más geométrico de
Newton. El trabajo de Leibniz tuvo un gran impacto en el desarrollo de las
matemáticas. El sacerdote jesuita francés Pierre Varignon (1654-1722)
aprendió el cálculo de Leibniz y lo usó para reelaborar los Principia de
Newton. Los dos hermanos suizos Jakob Bernoulli (1654-1705) y Johann
Bernoulli (1667-1748) también aprendieron cálculo de las publicaciones de
Leibniz y lo expandieron en nuevas direcciones. Johann Bernoulli lo utilizó
para resolver el problema de determinar la forma matemática de la cadena
colgante (catenaria). Un noble francés, el marqués de L'Hospital, contrató a
Johann Bernoulli para que le enseñara las nuevas matemáticas y luego publicó
lo que le enseñó como su propio texto de cálculo,
Analysis of the Infinitely Small (‘Análisis de lo infinitamente
pequeño’), en 1696. Era un texto de cálculo a partir del cual el tema se
puede aprender. Otro estudiante de los Bernoulli, el suizo Leonhard Euler
(1707-1783), se convirtió en el matemático más prolífico e influyente del
siglo XVIII. Su trabajo, unos increíbles 70 volúmenes en forma publicada,
avanzó el cálculo, desarrolló nuevos campos de las matemáticas y aplicó las
matemáticas para estudiar mecánica, artillería, música y barcos (y una serie
de otras materias). El cálculo variacional que introdujo Euler
es uno de los ingredientes clave en el poderoso
Método de Elementos Finitos (FEM) en el que se basa críticamente la
ingeniería moderna.
En referencia a su aplicación al análisis de estructuras, el cálculo es
mucho más que un método computacional que brinda soluciones a problemas
relevantes. Sus construcciones centrales están en sintonía con los conceptos
básicos que subyacen a nuestra comprensión de tales estructuras y brindan
información fundamental sobre ellas. Estos conceptos incluyen: volumen,
peso, fuerza, momento de fuerza y centro de masa.
La mecánica como ciencia intermedia entre la filosofía natural y las ciencias exactas
Desde la época de su “incipit” griego, la estática fue el origen de
una de las cuestiones más estimulantes de la filosofía natural y las
ciencias exactas. “La ciencia de los pesos está subordinada tanto a la
Geometría como a la Filosofía Natural”, escribió un anónimo autor medieval
de un comentario sobre el Elementa Arismeticae del matemático del
siglo XII Giordano Nemorario.
La misma tesis fue expresada por otros científicos al comienzo de la era
moderna: La estática se colocó en un nivel distinguido en comparación con
otras ciencias, en algún lugar entre la investigación física y las
matemáticas puras. En los siglos XVIII y XIX cambió el lenguaje, pero no el
concepto. Los autores más famosos atribuyeron gran importancia no solo a la
Estática sino también a toda la Mecánica, ubicándolas de últimas en el campo
de las Matemáticas y de primeras entre las Ciencias Naturales. Es bajo esta
luz que debe verse el “gran problema metafísico” (para usar las palabras de
D'Alembert) planteado en el siglo XVIII por la Academia de Ciencias de
Prusia. La cuestión de “si las leyes de la Estática y la Mecánica son de hecho necesarias o
contingentes” fue discutida desde varios puntos de vista, pero con el mismo propósito,
por Daniel Bernoulli, Euler y D'Alembert. El mismo espíritu impregna las
obras de Lagrange, Laplace, Poisson y Carnot, así como muchas otras.
Desde un punto de vista histórico, siempre se ha pensado que los principios
de la Estática tenían dos atributos: estos eran a la vez proposiciones de
relevancia empírica y teoremas de un sistema deductivo cuyos axiomas eran
tan obvios que no requerían de confirmación específicas. Este no fue el
único dualismo; el otra era si la estática podía ser tratada como un caso
extremo y anómalo de la dinámica, y en este sentido estaba subordinada a
ella, o si, por otro lado, estaba en la naturaleza de las cosas que la
dinámica se basara en la estática.
Teorías de la Fricción en el Siglo XVIII
A diferencia de la memoria teórica de 1773 sobre problemas de resistencia de
materiales, mecánica de suelos y diseño de arcos, el estudio de fricción de
Coulomb contenía tanto un análisis racional de los problemas como los
resultados de extensas pruebas de ingeniería. La “Teoría de las máquinas
simples” está más cerca de la tradición de la ingeniería del siglo XVIII que
cualquiera de los otros estudios de Coulomb. Quizás solo por esta razón se
convirtió en su memoria de ingeniería más famosa. No muestra la brillantez de
su Memoria sobre Estática de 1773, pero se ocupó de un fenómeno complicado y
muy difícil de examinar.
La fricción es el estudio de las interacciones superficiales de los cuerpos.
Los efectos de este fenómeno se han observado desde la antigüedad, pero la
tradición del estudio cuantitativo de sus parámetros comenzó solo a fines del
siglo XVII. Hay tres fases importantes en el desarrollo temprano de las
teorías de la fricción:
- Los experimentos iniciales y la teoría de Amontons (1699) (Amontons, Guillaume. “De la résistance causée dans les machines,” Mémoires de l'Académie Royale des Sciences, 1699 (Paris, 1718), pp. 206-227),
- la adición de Desaguliers de la idea de cohesión o atracción molecular (1725) (Desaguliers, J. T. “Some Experiments Concerning the Cohesion of Lead,” Philosophical Transactions, XXXIII (London, 1725), 345-347) y,
- el trabajo de Coulomb (1781) (1781 friction memoir. “Theorie des machines simples en ayant égard au frottement de leurs parties et à la roideur des cordages ... ,” X (Paris, 1785), pp. 161-332. (Reprinted in Théorie des machines simples…).
El desarrollo de Parent y Euler de la teoría de Amontons en términos de
mecánica racional contribuyó bastante poco al conocimiento de la fricción.
Coulomb combinó una teoría generalizada con la única serie extensa y
satisfactoria de experimentos realizados hasta mediados del siglo XIX. En su
Memoria sobre Estática de 1773, Coulomb aceptó la teoría de Amontons, pero
siguiendo a Bossut notó que el coeficiente de fricción podría variar con los
materiales utilizados. Descubrió que podía ser 3/4 en el caso de ladrillos de
arcilla y que para el granito y otras piedras de construcción variaba con cada
piedra individual.
Se han asignado observaciones de fricción y esfuerzos para mitigar sus efectos
a los egipcios, griegos y romanos; y Leonardo da Vinci aparentemente realizó
experimentos sobre fricción y registró observaciones de estos en sus
cuadernos. Los autores del siglo XVIII fueron unánimes al reconocer el crédito
de Amontons para los primeros estudios de fricción; ninguno menciona ningún
estudio de los antiguos o de Leonardo, cuyos cuadernos permanecieron
desconocidos hasta el siglo XIX.
En su galardonada memoria de magnetismo de 1777, Coulomb investigó el diseño y
el montaje de pequeñas agujas magnéticas. Él intentó diseñar una brújula
precisa adecuada para su uso práctico en el servicio marítimo. Esto involucró
estudios de la fricción de pivote en agujas de brújula. Afirmó que la Ley de
Amontons no parecía ser válida para mecanismos pequeños. En las agujas de la
brújula, la fricción del pivote variaba aproximadamente como la potencia de
3/2 de la fuerza normal.
Aunque reconoció el valor práctico del trabajo de Amontons, Coulomb era
consciente del hecho de que era estrictamente aplicable solo a una clase
estrecha de cuerpos materiales que interactúan. Antes de poder construir una
teoría integral, sería necesario inaugurar una serie sistemática de
experimentos sobre fenómenos de fricción.
Estos experimentos implicarían la investigación de los efectos de todas las
variables posibles, y los experimentos con modelos a pequeña escala no serían
suficientes. La investigación llevaría un tiempo considerable y requeriría la
construcción de numerosas piezas de equipos de prueba grandes.
Fricción y Cohesión en la Memoria sobre Estática
Al comienzo del cuerpo del ‘Essai’, Coulomb introdujo tres proposiciones
básicas de la mecánica:
- PROPOSICIÓN I. Permítase que la figura plana abcde (ver Figura 2) que descansa sobre el plano AB sea actuada por cualquier fuerza plana. En equilibrio, la resultante de estas fuerzas será perpendicular a la línea AB y caerá entre los puntos base a y e.
- PROPOSICIÓN II. Si todas estas fuerzas se resuelven paralelas y perpendiculares a AB, la suma de fuerzas paralelas a AB será igual a cero y la suma de fuerzas perpendiculares a AB será igual al peso de la sección plana, P.
- PROPOSICIÓN III. Si se incluye la fuerza de reacción a P, las sumas de las fuerzas resueltas a lo largo de dos direcciones perpendiculares cualesquiera serán iguales a cero.
|
| Figura 2. Imagen de Coulomb que ilustra tres proposiciones básicas de la mecánica |
Estas tres proposiciones eran importantes para Coulomb, y las recordaba
constantemente en las secciones siguientes de la memoria. No son originales,
pero es inusual ver que se basen específicamente en la literatura de
ingeniería de ese período. Indican que Coulomb buscó soluciones generales
basadas en principios fundamentales de la mecánica estática. Una vez que
hubo establecido estas proposiciones, pasó a la
Mémoir.
El cálculo sirvió como un dispositivo para describir y resolver los
problemas de ingeniería que Coulomb trató. Sin embargo, el contenido de los
problemas se clasificó en dos categorías:
- La elasticidad y resistencia de los materiales,
- La mecánica estructural.
La consideración de la fricción y la cohesión fue central en esta
investigación, y lo involucró a brindar virtualmente en la primera mitad de
su trabajo, una teoría de la flexión de vigas y la ruptura y corte de
materiales frágiles. La segunda mitad de la memoria se dedicó a los
problemas de mecánica estructural de la presión de tierra en los muros de
contención y la estabilidad de los arcos.
El método utilizado por Coulomb fue el mismo para todos los problemas que
estudió. Los fenómenos complejos de estática convertidos en problemas
físicos podrían dar al físico solo una idea aproximada de su efecto. Los
factores físicos individuales como el cizallamiento, la fricción del arco o
la forma de la cuña de presión de tierra no se podían calcular con
precisión. Coulomb buscó determinar los límites de su acción. A lo largo de
la memoria, dejó que los factores desconocidos variaran y resolvieran el
valor límite de la presión en el punto entre el equilibrio y la ruptura. Se
ocupó de manera similar con la presión de tierra, la ruptura por compresión
en las columnas y la estabilidad de los arcos. Es bastante incidental que
haya tratado la flexión de las vigas, pero todas estas soluciones requerían
valores para los efectos físicos: fricción y cohesión.
La fricción y la cohesión debían considerarse conforme al papel que
desempeñan en las interacciones físicas reales. Mientras la física se
refleje en el mundo ideal de análisis o en las tablas tradicionales de
ingeniería empírica, la fricción y la cohesión podrían pensarse o agruparse
en un resultado observado. Sin embargo, estas propiedades de interacción
material preocuparon al investigador del siglo XVIII. Desde cualquier
extremo del espectro, el empirismo tradicional o el análisis puro, los
intentos de lidiar con los materiales en sus interacciones no tendrían éxito
si no se buscaba una teoría o si la teoría era un intento demasiado
simplificado para reflejar las armonías de la naturaleza.
Para el mecánico aplicado, la fricción y la cohesión son los vínculos entre
la geometría y la realidad física. Coulomb obtuvo una teoría exitosa de la
fricción, exitosa al menos en que parecía explicar los fenómenos y en que se
estableció como la teoría clásica. Continuó estudiando la fricción a lo
largo de su carrera científica como se encuentra en la literatura técnica.
La cohesión, por otro lado, fue vista como bastante diferente. En la Memoria
sobre Estática de 1773, en el ensayo de 1781 sobre la fricción en máquinas
simples, y en otras memorias, se estudió el papel de la cohesión, aunque sus
efectos en los fenómenos de fricción fueron muy difíciles de medir.
Coulomb a menudo asociaba la fricción con el mecanismo de corte, aunque
nunca lo definió explícitamente así, ni usó el término. Cuando un cuerpo se
movía sobre la superficie de otro, Coulomb imaginó que cortaba pequeñas
irregularidades o las doblaba. La cohesión generalmente la veía en términos
de resistencia a la tracción o a la compresión o de corte. Los términos
cohérence, adhérence y cohésion fueron utilizados por
Coulomb y la mayoría de los escritores del siglo XVIII para describir los
mismos fenómenos generales. Una viga, por ejemplo, cargada a tracción
resistiría la ruptura hasta un cierto límite en el cual se excederían las
fuerzas cohesivas que mantienen unidas las moléculas y la viga se rompería.
Cuando Coulomb se ocupó de la ruptura por compresión de las columnas o la
ruptura por tracción de la piedra, utilizó el término cohesión en este
sentido. Cuando habló de cizallamiento torsional a nivel molecular en
metales, la cohesión también se vio como la fuerza que mantiene unidas las
moléculas hasta la ruptura debido al cizallamiento. Para ambos casos, de
fricción y de cohesión, sea lo que sea que Coulomb haya inferido de sus
experimentos, obtuvo resultados cuantitativos a escala macroscópica. Es
decir, obtuvo coeficientes cuantitativos y leyes de fricción que son válidas
para situaciones macroscópicas. Aunque puede haber especulado sobre la
estructura molecular, no obtuvo resultados cuantitativos aplicables a nivel
de interacción molecular individual.
En el siglo XVIII, la fricción y la cohesión se consideraban conceptos
opuestos (Figura 3), donde la fuerza de fricción Ff es
proporcional a la fuerza normal P; y la fuerza de cohesión
Fc es inversamente proporcional a alguna función de la
distancia de separación, d, para d muy pequeña y con el
exponente n mayor que 2
|
| Figura 3. Representación de C. S. Gillmor (1971) de las concepciones del siglo XVIII de los mecanismos de fricción y cohesión |
La fricción podría imaginarse como una acción de contacto en la que un
cuerpo colisionaba a nivel molecular de alguna manera con otro, aunque la
interacción parecía tangencial a gran escala. Sin embargo, la cohesión no
implicaba necesariamente una acción de contacto, sino solo el acercamiento
cercano de un cuerpo a otro. Impulsados por su interpretación de la
Consulta XXXI de la Opticks de Newton, el filósofo francés Jean
Theophile Desaguliers (1683-1744) especialmente, y otros, intentarían ver
en la naturaleza pruebas de fuerzas de atracción cohesivas que actuaran a
distancias muy pequeñas y que posiblemente siguieran una ley de atracción
distinta de la ley de gravitación de los inversos cuadrados con respecto a
la distancia de separación de los cuerpos. En otras palabras, podría haber
alguna ley de fuerza de acción cercana que variara como el cubo inverso o
alguna otra potencia de la distancia. Coulomb nunca propuso identificar
ninguna ley de este tipo. Mientras la fricción dependiera de la fuerza
normal que actuaba entre dos cuerpos en lugar del área superficial común
de interacción, esto implicaba la teoría de la rugosidad superficial. En
la medida en que la fricción dependiera del área de la superficie en
contacto, podría implicar fuerzas cohesivas como pensaba Desaguliers, o
los efectos de la película superficial que Coulomb suponía como una
alternativa.
En cualquier caso, los experimentos de Coulomb en fricción mostraron que
el efecto del área superficial siempre fue inferior al pequeño porcentaje
de la fricción total para cualquier situación en la que las fuerzas
normales ascendían a varias libras o más.
En los artículos IV y V de la memoria sobre estática de 1773, Coulomb
señaló que la fricción y la cohesión se miden por los límites de su
resistencia. Es decir, nunca son fuerzas activas como la gravedad, sino
fuerzas “coercitivas”. Aquí, aceptó la
teoría de la fricción de Amontons, de que entre cuerpos es
principalmente proporcional a la fuerza que actúa normal a la superficie
de contacto de los cuerpos y no a su área superficial. Sin embargo, señaló
que esta ley de fricción no se observa estrictamente y que, con materiales
no fibrosos, como la piedra, es necesario ensayar el coeficiente de
fricción de cada tipo de piedra que se usaría porque “las pruebas realizadas para una cantera pueden nunca servir para
otra”. Para la muestra de piedra que probó, Coulomb encontró que el
coeficiente de fricción era igual a 3/4.
La cohesión, según Coulomb, se mide por la resistencia a la que los
cuerpos sólidos se oponen a la “desunión” directa de sus partes. En un
cuerpo homogéneo, cada parte resiste la ruptura con el mismo grado de
resistencia. Por lo tanto, la cohesión total es proporcional al número de
partes a ser separadas y, por lo tanto, al área superficial de ruptura.
Para determinar la cantidad de cohesión en el material frágil, Coulomb
empleó un bloque de piedra blanca de Burdeos cortada y suspendida como se
muestra en la Figura 4, de modo que el área a romper era igual a dos
pulgadas cuadradas. Cargó esta piedra hasta que se produjo la ruptura, a
un valor de 430 libras. Luego, fijó una losa de piedra de sección
transversal similar y la sometió a una fuerza de corte pura que resultó en
una ruptura de 440 libras. Después de varios ensayos, concluyó que la
fuerza necesaria para producir la ruptura por cizallamiento fue siempre
una cantidad ligeramente superior que la que produjo la ruptura por
tracción. Sobre la base de estos resultados experimentales, supuso que la
cohesión para materiales frágiles era casi la misma a lo largo de
cualquier plano de ruptura. Recordando sus experimentos en Martinica,
advirtió que las condiciones climáticas afectaron en gran medida la
resistencia a la rotura del mortero y que, al igual que con la fricción,
uno debe ensayar una muestra de cada tipo de piedra de construcción antes
de comenzar los cálculos de diseño. Así, habiendo obtenido coeficientes de
fricción y “cohesión” en piedra, procedió a una investigación de la
flexión de vigas.
|
|
Figura 4. Representación de C. S. Gillmor (1971) del aparato
experimental de Coulomb para ensayos de rotura por tracción en
piedra (izquierda) y piedra caliza blanca de Bordeaux (centro y
derecha) |
Los trabajos de investigación de Coulomb y Amontons y las leyes
generalizadas de la fricción
Con frecuencia se afirma que fue Leonardo da Vinci (1452-1519) quien hizo
la primera contribución significativa a la física de la fricción mediante
la formulación de las principales “leyes de fricción seca”:
(a) La fricción es proporcional al peso,
(b) la fricción no depende del área de contacto, y
(c) la relación de fricción a peso es aproximadamente 1/4.
Sin embargo, estas conclusiones fueron escritas en sus cuadernos
personales y no parecen haber tenido ningún impacto en la ciencia y la
ingeniería de ese momento. El primer estudio de fricción que fue
ampliamente discutido en público parece ser la memoria de 1699 presentada
a la Academia de Ciencias
De la resistance cause’e dans les machines ('De la resistencia
provocada en las máquinas') de Guillaume Amontons (1663-1705) (Figura 5).
Justo al comienzo de su memoria, Amontons formula las siguientes cuatro
“leyes de fricción”:
- Primero, la resistencia causada por la fricción aumenta / disminuye en proporción a la presión.
- Segundo, la resistencia causada por la fricción es la misma para el hierro, el cobre, el plomo y la madera siempre que estén lubricados con una grasa.
- Tercero, esta resistencia es aproximadamente igual a un tercio de la presión.
- Cuarto, esta resistencia no depende de la velocidad y otras condiciones.
|
|
Figura 5. Dispositivo de fricción (arriba izquierda) de g.
Amontons (izquierda) y extractos de la memoria ‘De la resistance
cause’e dans les machines’ de 1699: (a) página de título, y (b)
formulación de las “leyes de fricción” (derecha) |
Esta es la formulación clásica de la ley de la fricción seca, como se encuentra en la mayoría de los libros escolares contemporáneos
sobre física. El trabajo de Amontons se hizo ampliamente conocido y tuvo
un gran impacto en la práctica de la ingeniería. La proporcionalidad de la
fuerza de fricción a la fuerza normal se llama, con razón, “Ley de
Amontons”. El gran mérito de Amontons fue la simplificación del muy
complejo fenómeno de la fricción seca. Su ley de fricción era de
“naturaleza empírica cruda”, porque en ese momento no había ideas
adecuadas que pudieran conducir a una “derivación” apropiada o comprensión
teórica de esta ley. Incluso hoy, surgen periódicamente discusiones muy
emocionales sobre la naturaleza física de la ley de Amontons. Al mismo
tiempo, no se debe olvidar que la generalidad de la “ley de Amontons” se debe a su extrema “aspereza”: es una aproximación de orden cero que
describe la realidad solo cualitativamente, pero se vuelve incorrecta tan
pronto como se requiere información más detallada acerca de la fricción.
Una comprensión mucho mejor del fenómeno de fricción en toda su
complejidad se debe a los trabajos de Charles Augustin Coulomb.
Las obras de Coulomb sobre la fricción: un breve panorama histórico
Además de las obras originales de Coulomb, el ensayo histórico más
completo sobre su vida y obra se puede encontrar en el libro de Gillmor de
1971 (Coulomb and the Evolution of Physics and Engineering in
Eighteenth-Century France).
El primer trabajo científico de Coulomb fue su memoria de 1773 “Essai sur une Application des Règles de Maximis et Minimis á quelques
Problemes de Statique, relatifs à l’Architecture” ('On an application of the rules of maximum and minimum to some
statical problems, relevant to architecture' (en
inglés) o 'Sobre la aplicación de las reglas de máximo y mínimo a algunos
problemas estáticos, relevantes para la arquitectura' (en español)). En
los primeros párrafos de su memoria, Coulomb escribe:
“El objetivo de este trabajo es determinar, en la medida en que lo
permita una mezcla de cálculo y principios físicos, el efecto de la
fricción y de la cohesión en algunos problemas de estática”.
En este trabajo, Coulomb consideró solo la fricción estática. Él escribe:
“La fricción y la cohesión no son fuerzas activas como la gravedad, que
siempre ejerce su pleno efecto, sino solo fuerzas pasivas; estas dos
fuerzas se pueden medir por los límites de su resistencia ... Asumiré
aquí que la resistencia debida a la fricción es proporcional a la fuerza
de compresión, como fue encontrado por Amontons, aunque para los cuerpos
grandes la fricción no sigue exactamente esta ley. De acuerdo con esta
suposición, se encuentra que la fricción para los ladrillos es tres
cuartas partes de la fuerza de compresión
...”
(Sección IV del ‘Essai’).
Sin embargo, el foco de esta primera memoria de Coulomb no fue sobre la
fricción, sino sobre la mecánica y la resistencia de los materiales,
estudios realizados por Coulomb en Martinica, donde estuvo a cargo de la
construcción del nuevo Fort Bourbon. Desde el punto de vista de la forma
de presentación y los medios matemáticos utilizados, esta primera
publicación de Coulomb es muy similar a los libros de texto modernos sobre
la mecánica de materiales. Por ejemplo, al tratar la resistencia de las
columnas, primero considera secciones de la columna orientadas de forma
diferente bajo el supuesto de cohesión que no depende de la fuerza de
compresión. Encuentra la sección con el máximo esfuerzo tangencial
estableciendo la derivada del esfuerzo con respecto al ángulo a cero y
llega a la conclusión de que las columnas fallarán debido al corte a lo
largo de caras orientadas a 45° con respecto al eje de la columna. Luego
generaliza su tratamiento al introducir una resistencia al corte que tiene
componentes cohesivos y de fricción, siendo este último proporcional a la
fuerza de compresión. En la notación contemporánea, escribiríamos su
suposición como
La ecuación (1) es muy utilizada en la mecánica de medios (continuos) y
suelos granulares y, se denomina históricamente de forma correcta como
Criterio de Falla de Coulomb. Es interesante notar que esta ley de resistencia/fricción de “dos
componentes” también fue explotada por Coulomb en sus trabajos
posteriores. Por lo tanto, consideró “resistencia” y “fricción estática”
desde el mismo punto de vista. La diferencia estaba solo en la importancia
relativa de las contribuciones cohesivas y friccionales.
En 1779, Coulomb fue transferido a Rochefort para participar en la
construcción de un fuerte hecho completamente de madera cerca de Ile
d'Aix, donde tuvo la posibilidad de usar un laboratorio para sus
investigaciones. Durante este período, Coulomb llevó a cabo una serie de
experimentos dedicados al estudio de la fricción, cuyos resultados fueron
presentados en la memoria “Theorie des Machines Simples, En Ayant egard au frottement de leurs
parties, et a la roideur des Cordages” (“La teoría de las máquinas simples”): el trabajo seminal en el estudio
de la fricción. En 1781 Coulomb recibió un premio de la Academia de
Ciencias parisina por este trabajo. Este fue el segundo premio de la
Academia ganado por Coulomb.
En años posteriores, Coulomb regresó muchas veces a estudios de fricción.
En julio de 1789 presentó su estudio sobre la fricción en pivotes de punta
y fricción de rodadura. En 1780 también estudió la fricción en fluidos.
Encontró, correctamente, que la fuerza de fricción en los fluidos es
proporcional a la velocidad a velocidades muy pequeñas y al cuadrado de
velocidad a mayores velocidades, y no depende de la rugosidad de los
sólidos que están en contacto con el fluido. En el caso de los fluidos,
también sugirió que existe una parte de fricción “cohesiva” que no depende
de la velocidad. Sin embargo, no pudo determinarlo experimentalmente. Es
interesante observar que esta intuición resultó ser parcialmente correcta,
ya que, en algunos “fluidos”, uno realmente puede identificar partes de
fricción estáticas y viscosas (por ejemplo, en elastómeros blandos o
lubricación con grasa).
Principales hallazgos de Coulomb con respecto a la fricción seca
Coulomb comienza su principal libro de memorias sobre la fricción (Figura
6) con esta declaración introductoria:
“Amontons parece ser el primer autor que intentó evaluar la fricción y
la rigidez de las cuerdas para calcular las máquinas. Creyó que había
descubierto a través de sus experimentos que la extensión de las
superficies no influye en la fricción, que depende únicamente de la
presión de las partes en contacto: concluye que, en todos los casos, la
fricción es proporcional a la presión.”
|
|
Figura 6. El trabajo principal de Coulomb dedicado a la
fricción: “Théorie des machines simples”, edición
parisina de 1821: (a) portada, (b) Comienzo de la memoria. En
recuadro: a) Modelo de fricción de Coulomb; b) Modelo de Coulomb
con resorte en serie |
Luego, concluye que otras investigaciones muestran que la ley de Amontons
es inexacta y que una investigación detallada es importante. Coulomb
investigó la fuerza de la fricción en función de muchos factores, que
Gillmor (1971) resume en la siguiente lista:
- materiales que constituyen los cuerpos que reaccionan;
- condiciones de la superficie (pulido, rugoso);
- lubricantes (aceite, sebo, alquitrán, grasa para ejes, agua);
- peso (fuerza normal);
- área de superficie de contacto;
- efectos de deformación o cohesión debido al tiempo de reposo;
- orientación geométrica de las superficies que interactúan (paralelas o perpendiculares a la veta de la madera, etc.);
- velocidad del movimiento de la superficie;
- deformación debido a la geometría de las superficies (forma de las superficies que interactúan: plana, puntiaguda, curva);
- temperatura y humedad;
- estado de movimiento (uniforme o impulsivo);
- presión del aire.
La investigación de Coulomb es un ejemplo de excelente trabajo
experimental, que aparentemente no fue guiado por ninguna idea puramente
teórica o reglas simples. Él “honestamente” estudió la fuerza de la
fricción bajo diversas condiciones e intentó presentar los resultados en
una forma que puede ser utilizada por físicos e ingenieros.
Dependencia de la fuerza de fricción estática en el tiempo de contacto
Coulomb sabía que la fuerza estática de la fricción depende del tiempo
transcurrido desde el primer momento de contacto. Por lo tanto,
nunca da el valor de la fuerza de fricción estática sino
tres o cuatro valores: por ejemplo, después de 1/2 seg, 2 seg, 10 seg y 1
hora (Figura 7). La última declaración significa que la fuerza de fricción
alcanza su nivel estacionario después de 10 segundos y no cambia más.
|
|
Figura 7. Presentación típica de los datos sobre la fuerza de
fricción en la “Théorie des machine simples”. Los valores
para cada fuerza normal se dan para diferentes tiempos de espera
hasta el momento de la saturación |
Dependencia de la fuerza de fricción deslizante sobre la fuerza normal
Coulomb también estudió la dependencia del coeficiente de fricción
deslizante con la fuerza normal. Coulomb nunca usó la noción de
“coeficiente de fricción”, pero a menudo presenta la relación de la fuerza
normal con la fuerza de fricción, el “coeficiente de fricción inverso” (Figura 8). Se aprecia que, al aumentar la fuerza normal en un factor
de 35, Coulomb observa una disminución del coeficiente de fricción casi en
un factor de dos. En otros ejemplos, observó incluso una mayor dependencia
de la fuerza normal.
|
|
Figura 8. Dependencia del coeficiente de fricción inverso en la
fuerza normal. “Fricción de una superficie de un pie cuadrado y
las siguientes cargas” |
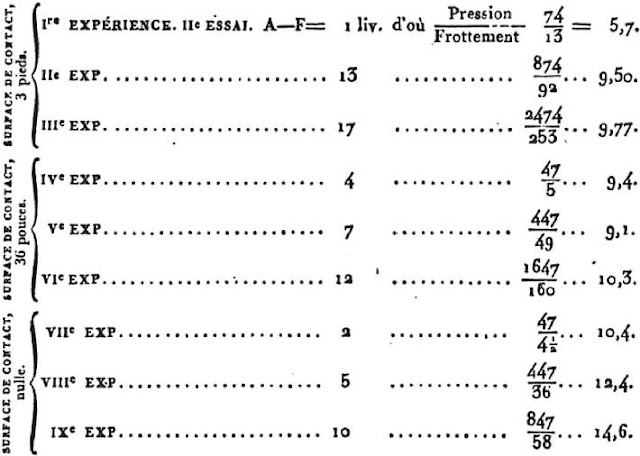
Dependencia de la fuerza de fricción en el tamaño de contacto
Coulomb encuentra que en la mayoría de los casos la fuerza de fricción no
es muy sensible al área de contacto, como ya lo ha encontrado Amontons.
Sin embargo, en algunos casos, encontró una dependencia pronunciada
(Figura 9).
|
|
Figura 9. Dependencia del coeficiente de fricción inverso en el
área de contacto, un ejemplo de los datos de Coulomb |
Dependencia de otros parámetros
Coulomb también estudió la influencia de muchos otros factores y trató de
resumirlos en una forma que pudiera ser utilizada por los ingenieros. En
la mayoría de los casos, logró formular leyes simples de “dos términos”
del mismo tipo que la ecuación (1) donde el primer término describió la
contribución constante principal y el segundo una dependencia
relativamente débil de la variable en cuestión (tiempo, fuerza normal,
velocidad, tamaño del contacto, etc.).
Los principales hallazgos de Coulomb sobre la dependencia de la fuerza de
fricción en la fuerza normal y el tamaño de contacto aparente se pueden
resumir de la siguiente manera:
El coeficiente de fricción para el par de fricción dado se hace más
grande, si la profundidad de indentación de la rugosidad de dos cuerpos
se vuelve más pequeña
(fuerzas más pequeñas, área de contacto más grande).
Sin embargo, Coulomb hizo solo generalizaciones empíricas muy generales:
- “Al deslizar la madera sobre la madera sin lubricación, después de un largo período de contacto, la fuerza de fricción es directamente proporcional a la presión normal; esta fuerza aumenta solo en los primeros momentos de contacto, después de unos minutos alcanza un máximo.”
- “Al deslizar madera sobre madera sin lubricante a cierta velocidad, la fuerza de fricción también es proporcional a la presión normal, pero, incluso en su forma más grande, es mucho menor que la requerida para romper la unión entre las superficies después de un tiempo de contacto. Por ejemplo, se establece que la fuerza necesaria para interrumpir el contacto entre dos superficies de roble, después de algunos minutos de contacto, se refiere a la fuerza requerida para vencer la fricción cuando la superficie se mueve con una velocidad determinada de 35:22.”
- “Cuando el metal se desliza sobre metal sin lubricación, la fuerza de fricción es proporcional a la presión, pero su valor es el mismo, independientemente de si quieren perturbar la relación entre las superficies después de un tiempo de contacto, o si desean mantener una cierta velocidad constante.”
- “Los resultados del deslizamiento de superficies diferentes, como la madera sobre metal, sin lubricante, difieren considerablemente de los anteriores, ya que la intensidad de la fricción, dependiendo de la duración del contacto, aumenta lentamente y alcanza su punto máximo después de 4 a 5 días, y algunas veces más, mientras que para los metales alcanza el valor estacionario en un instante y para la madera en pocos minutos; este crecimiento es tan lento que la resistencia de fricción a velocidades muy bajas es casi la misma que en la falla de contacto por agitación o separación después de 3 o 4 s de contacto. Además, para la madera que se desliza sobre la madera sin lubricante y para el deslizamiento del metal sobre el metal, la velocidad afecta la fricción solo muy débilmente: en este caso, la fricción aumenta a medida que aumenta la velocidad; mientras la velocidad aumenta exponencialmente, la fricción aumenta en una progresión aritmética.”
Referencias
Benvenuto, E. (1991). An Introduction to the History of Structural
Mechanics. Part I: Statics and Resistance of Solids. Springer.
Benvenuto, E. (1991). An Introduction to the History of Structural
Mechanics. Part II: Vaulted Structures and Elastic Systems. Springer.
Coulomb, C. A. (1776). “Essai sur une Application des Règles de Maximis et
Minimis á quelques Problemes de Statique, relatifs à l’Architecture”. Mem.
Div. Sav. Académie des Sciences.
Bowden, F. P. & Tabor, D. (1964). “The Friction and Lubrication of
Solids, Part II,” Chapter XXIV, pp. 502516, Oxford, Clarendon Press.
Coulomb, C. A. (1779). nueva edición de 1821, Théorie des Machines Simples,
en ayant égard au frottement de leurs parties et a la rodieur des cordages,
Bachelier, Librairie, Quai del Augustins, Paris, pp 318-363.
Coulomb, C. A. (1785). “Theorie des Machines Simples, En Ayant egard au
frottement de leurs parties, et a la roideur des Cordages,” Memoires de
Mathematique et de Physique, Tome X, a Paris MDCCLXXXV, pp 161-342.
Hahn, A.J. (2012). Mathematical Excursions to the World's Great Buildings.
Princeton University Press.
de Boer, R. (2000). Theory of Porous Media: Highlights in Historical
Development and Current State. Springer. Verlag. Berlin. Heidelberg. New
York.
Dowson Duncan (1978). Men of Tribology. 148-Vol 100, april. Copyright 1978
by ASME Transactions of the ASME.
Falconer, I. (2204). “Charles Augustin Coulomb and the fundamental law of
electrostatics”. Institute of Physics Publishing. Metrologia 41 (2004)
S107–S114 PII: S0026-1394(04)83190-6.
Gauthier-Villars Publisher (1884). Collection de mémoires relatifs à la
physique by La Société Française de Physique. 1884. Collection European
libraries. French.
Gillmor, C. S. (1968). “Charles Augustin Coulomb: Physics and Engineering in
Eighteenth-Century France,” PhD dissertation, University of Princeton.
Gillmor, C. S. (1971). Coulomb and the Evolution of Physics and Engineering
in Eighteenth-Century France, Princeton University Press, Princeton, New
Jersey, U.S.A.
Heyman, J. (1972). Coulomb's Memoirs on Statics: An Essay in the History of
Civil Engineering. Cambridge, U.K.
Kragelsii, I. V. and Shchedrov, V. S. (1956). “Razvite Nauki o Treni,”
(Development of the Science of Friction). Chapter 4, Investigations by
Coulomb, Soviet Academy of Sciences, Moscow.
Magee, W. S. (1963). “Historic Researches; No. 1. Friction—Coulomb and
Morin's Experiments,” The Engineer, p. 22, July 14,1944.
Miller, D. (2014). Physicists (Great Scientists). Cavendish Square LLC.
Popova, E. Popov, V. L. (2015). The research works of Coulomb and Amontons
and generalized laws of friction. Friction 3(2): 183–190 (2015).
Sarhosis, V., Bagi, K., Lemos, J.V., Milani, G. (eds.). (2016).
Computational Modeling of Masonry Structures Using the Discrete Element
Method. IGI Global.
Sinopoli, A. (2002). A Re-examination of Some Theories on Vaulted
Structures: The Role of Geometry from Leonardo to de La Hire. Birkhäuser.
Cita
Osorio, S. (2021). L'essai de 1773 sur la statique - 2a
parte. Relatos de la Geotecnia. Blogger.com.
geotecnia-sor2.blogspot.com. https://geotecnia-sor2.blogspot.com/2021/10/essai-1773-2a-parte.html
Relatos de la Geotecnia
+ Apuntes de Geotecnia con Énfasis en Laderas
Ir a:
1 - Martinique, Antilles - France Février 1764 (Martinica, Antillas - Francia , febrero de 1764)
2 - Angoulême, province d'Angoumois - France 14 juin 1736 (Angoulême, provincia de Angumois - Francia, 14 de junio de 1736)
3 - Mézières, département des Ardennes - France 11 février 1760 (Mézières, departamento de Ardennes - Francia, 11 de febrero de 1760)
4 - Paris - France 10 mars 1773 (París - Francia, 10 de marzo de 1773)
5 - L'essai de 1773 sur la statique - 1a Parte (La Memoria sobre Estática de 1773 - 1a Parte)
7 - L'essai de 1773 sur la statique - 3a Parte (La Memoria sobre Estática de 1773 - 3a Parte)
8 - L'essai de 1773 sur la statique - 4a Parte (La Memoria sobre Estática de 1773 - 4a Parte)
9 - L'essai de 1773 sur la statique - 5a Parte (La Memoria sobre Estática de 1773 - 5a Parte)
10 - L'essai de 1773 sur la statique - 6a Parte (La Memoria sobre Estática de 1773 - 6a Parte)
11 - L'essai de 1773 sur la statique - 7a Parte (La Memoria sobre Estática de 1773 - 7a Parte)
12 - L'essai de 1773 sur la statique - 8a parte (La Memoria sobre Estática de 1773 - 8a Parte)
13 - La vie de Coulomb après l’Essai de 1773 (La vida de Coulomb posterior al 'Essai' de 1773)Apéndice A - Fuerte Bourbon (1765-1772)
Apéndice C - La Estática de las Siete Máquinas Simples
Apéndice D - La Statique (La Estática)
Apéndice E - Mécanique Classique (Mecánica Clásica)
Apéndice F - De la résistance des matériaux (De la Resistencia de Materiales)
Diseño: PatoMOP
2021
Comentarios
Publicar un comentario
Bienvenidos, agradezco sus comentarios ...